Massive Language fashions are comprised of billions of parameters (weights). For every phrase it generates, the mannequin has to carry out computationally costly calculations throughout all of those parameters.
Massive Language fashions settle for a sentence, or sequence of tokens, and generate a chance distribution of the subsequent most probably token.
Thus, usually decoding n tokens (or producing n phrases from the mannequin) requires operating the mannequin n variety of occasions. At every iteration, the brand new token is appended to the enter sentence and handed to the mannequin once more. This may be expensive.
Moreover, decoding technique can affect the standard of the generated phrases. Producing tokens in a easy manner, by simply taking the token with the best chance within the output distribution, may end up in repetitive textual content. Random sampling from the distribution may end up in unintended drift.
Thus, a strong decoding technique is required to make sure each:
- Excessive High quality Outputs
- Quick Inference Time
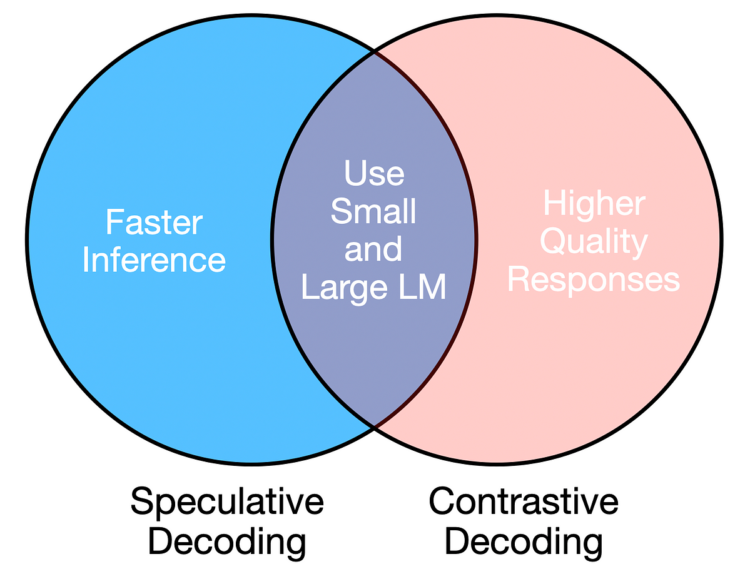
Each necessities might be addressed by utilizing a mixture of a giant and small language mannequin, so long as the beginner and knowledgeable fashions are related (e.g., similar structure however completely different sizes).
- Goal/Massive Mannequin: Predominant LM with bigger variety of parameters (e.g. OPT-13B)
- Beginner/Small Mannequin: Smaller model of Predominant LM with fewer parameters (e.g. OPT-125M)
Speculative and contrastive decoding leverage giant and small LLMs to realize dependable and environment friendly textual content era.
Contrastive Decoding is a method that exploits the truth that that failures in giant LLMs (corresponding to repetition, incoherence) are much more pronounced in small LLMs. Thus, this technique optimizes for the tokens with the best chance distinction between the small and enormous mannequin.
For a single prediction, contrastive decoding generates two chance distributions:
- q = logit chances for beginner mannequin
- p = logit chances for knowledgeable mannequin
The following token is chosen primarily based on the next standards:
- Discard all tokens that wouldn’t have sufficiently excessive chance beneath the knowledgeable mannequin (discard p(x) < alpha * max(p))
- From the remaining tokens, choose the one the with the biggest distinction between giant mannequin and small mannequin log chances, max(p(x) – q(x)).
Implementing Contrastive Decoding
from transformers import AutoTokenizer, AutoModelForCausalLM
import torch# Load fashions and tokenizer
tokenizer = AutoTokenizer.from_pretrained('gpt2')
amateur_lm = AutoModelForCausalLM.from_pretrained('gpt2')
expert_lm = AutoModelForCausalLM.from_pretrained('gpt2-large')
def contrastive_decoding(immediate, max_length=50):
input_ids = tokenizer(immediate, return_tensors="pt").input_ids
whereas input_ids.form[1] < max_length:
# Generate beginner mannequin output
amateur_outputs = amateur_lm(input_ids, return_dict=True)
amateur_logits = torch.softmax(amateur_outputs.logits[:, -1, :], dim=-1)
log_probs_amateur = torch.log(amateur_logits)
# Generate knowledgeable mannequin output
expert_outputs = expert_lm(input_ids, return_dict=True)
expert_logits = torch.softmax(expert_outputs.logits[:, -1, :], dim=-1)
log_probs_exp = torch.log(expert_logits)
log_probs_diff = log_probs_exp - log_probs_amateur
# Set an alpha threshold to remove much less assured tokens in knowledgeable
alpha = 0.1
candidate_exp_prob = torch.max(expert_logits)
# Masks tokens beneath threshold for knowledgeable mannequin
V_head = expert_logits < alpha * candidate_exp_prob
# Choose the subsequent token from the log-probabilities distinction, ignoring masked values
token = torch.argmax(log_probs_diff.masked_fill(V_head, -torch.inf)).unsqueeze(0)
# Append token and accumulate generated textual content
input_ids = torch.cat([input_ids, token.unsqueeze(1)], dim=-1)
return tokenizer.batch_decode(input_ids)
immediate = "Massive Language Fashions are"
generated_text = contrastive_decoding(immediate, max_length=25)
print(generated_text)
Speculative decoding relies on the precept that the smaller mannequin should pattern from the identical distribution because the bigger mannequin. Thus, this technique goals to just accept as many predictions from the smaller mannequin as doable, supplied they align with the distribution of the bigger mannequin.
The smaller mannequin generates n tokens in sequence, as doable guesses. Nonetheless, all n sequences are fed into the bigger knowledgeable mannequin as a single batch, which is quicker than sequential era.
This ends in a cache for every mannequin, with n chance distributions in every cache.
- q = logit chances for beginner mannequin
- p = logit chances for knowledgeable mannequin
Subsequent, the sampled tokens from the beginner mannequin are accepted or rejected primarily based on the next circumstances:
- If chance of the token is larger in knowledgeable distribution (p) than beginner distribution (q), or p(x) > q(x), settle for token
- If chance of token is decrease in knowledgeable distribution (p) than beginner distribution (q), or p(x) < q(x), reject token with chance 1 – p(x) / q(x)
If a token is rejected, the subsequent token is sampled from the knowledgeable distribution or adjusted distribution. Moreover, the beginner and knowledgeable mannequin reset the cache and re-generate n guesses and chance distributions p and q.
Implementing Speculative Decoding
from transformers import AutoTokenizer, AutoModelForCausalLM
import torch# Load fashions and tokenizer
tokenizer = AutoTokenizer.from_pretrained('gpt2')
amateur_lm = AutoModelForCausalLM.from_pretrained('gpt2')
expert_lm = AutoModelForCausalLM.from_pretrained('gpt2-large')
# Pattern subsequent token from output distribution
def sample_from_distribution(logits):
sampled_index = torch.multinomial(logits, 1)
return sampled_index
def generate_cache(input_ids, n_tokens):
# Retailer logits at every step for beginner and knowledgeable fashions
amateur_logits_per_step = []
generated_tokens = []
batch_input_ids = []
with torch.no_grad():
for _ in vary(n_tokens):
# Generate beginner mannequin output
amateur_outputs = amateur_lm(input_ids, return_dict=True)
amateur_logits = torch.softmax(amateur_outputs.logits[:, -1, :], dim=-1)
amateur_logits_per_step.append(amateur_logits)
# Sampling from beginner logits
next_token = sample_from_distribution(amateur_logits)
generated_tokens.append(next_token)
# Append to input_ids for subsequent era step
input_ids = torch.cat([input_ids, next_token], dim=-1)
batch_input_ids.append(input_ids.squeeze(0))
# Feed IDs to knowledgeable mannequin as batch
batched_input_ids = torch.nn.utils.rnn.pad_sequence(batch_input_ids, batch_first=True, padding_value=0 )
expert_outputs = expert_lm(batched_input_ids, return_dict=True)
expert_logits = torch.softmax(expert_outputs.logits[:, -1, :], dim=-1)
return amateur_logits_per_step, expert_logits, torch.cat(generated_tokens, dim=-1)
def speculative_decoding(immediate, n_tokens=5, max_length=50):
input_ids = tokenizer(immediate, return_tensors="pt").input_ids
whereas input_ids.form[1] < max_length:
amateur_logits_per_step, expert_logits, generated_ids = generate_cache(
input_ids, n_tokens
)
accepted = 0
for n in vary(n_tokens):
token = generated_ids[:, n][0]
r = torch.rand(1).merchandise()
# Extract chances
p_x = expert_logits[n][token].merchandise()
q_x = amateur_logits_per_step[n][0][token].merchandise()
# Speculative decoding acceptance criterion
if ((q_x > p_x) and (r > (1 - p_x / q_x))):
break # Reject token and restart the loop
else:
accepted += 1
# Verify size
if (input_ids.form[1] + accepted) >= max_length:
return tokenizer.batch_decode(input_ids)
input_ids = torch.cat([input_ids, generated_ids[:, :accepted]], dim=-1)
if accepted < n_tokens:
diff = expert_logits[accepted] - amateur_logits_per_step[accepted][0]
clipped_diff = torch.clamp(diff, min=0)
# Pattern a token from the adjusted knowledgeable distribution
normalized_result = clipped_diff / torch.sum(clipped_diff, dim=0, keepdim=True)
next_token = sample_from_distribution(normalized_result)
input_ids = torch.cat([input_ids, next_token.unsqueeze(1)], dim=-1)
else:
# Pattern immediately from the knowledgeable logits for the final accepted token
next_token = sample_from_distribution(expert_logits[-1])
input_ids = torch.cat([input_ids, next_token.unsqueeze(1)], dim=-1)
return tokenizer.batch_decode(input_ids)
# Instance utilization
immediate = "Massive Language fashions are"
generated_text = speculative_decoding(immediate, n_tokens=3, max_length=25)
print(generated_text)
Analysis
We will consider each decoding approaches by evaluating them to a naive decoding methodology, the place we randomly decide the subsequent token from the chance distribution.
def sequential_sampling(immediate, max_length=50):
"""
Carry out sequential sampling with the given mannequin.
"""
# Tokenize the enter immediate
input_ids = tokenizer(immediate, return_tensors="pt").input_idswith torch.no_grad():
whereas input_ids.form[1] < max_length:
# Pattern from the mannequin output logits for the final token
outputs = expert_lm(input_ids, return_dict=True)
logits = outputs.logits[:, -1, :]
chances = torch.softmax(logits, dim=-1)
next_token = torch.multinomial(chances, num_samples=1)
input_ids = torch.cat([input_ids, next_token], dim=-1)
return tokenizer.batch_decode(input_ids)
To guage contrastive decoding, we will use the next metrics for lexical richness.
- n-gram Entropy: Measures the unpredictability or range of n-grams within the generated textual content. Excessive entropy signifies extra various textual content, whereas low entropy suggests repetition or predictability.
- distinct-n: Measures the proportion of distinctive n-grams within the generated textual content. Increased distinct-n values point out extra lexical range.
from collections import Counter
import mathdef ngram_entropy(textual content, n):
"""
Compute n-gram entropy for a given textual content.
"""
# Tokenize the textual content
tokens = textual content.break up()
if len(tokens) < n:
return 0.0 # Not sufficient tokens to kind n-grams
# Create n-grams
ngrams = [tuple(tokens[i:i + n]) for i in vary(len(tokens) - n + 1)]
# Rely frequencies of n-grams
ngram_counts = Counter(ngrams)
total_ngrams = sum(ngram_counts.values())
# Compute entropy
entropy = -sum((rely / total_ngrams) * math.log2(rely / total_ngrams)
for rely in ngram_counts.values())
return entropy
def distinct_n(textual content, n):
"""
Compute distinct-n metric for a given textual content.
"""
# Tokenize the textual content
tokens = textual content.break up()
if len(tokens) < n:
return 0.0 # Not sufficient tokens to kind n-grams
# Create n-grams
ngrams = [tuple(tokens[i:i + n]) for i in vary(len(tokens) - n + 1)]
# Rely distinctive and whole n-grams
unique_ngrams = set(ngrams)
total_ngrams = len(ngrams)
return len(unique_ngrams) / total_ngrams if total_ngrams > 0 else 0.0
prompts = [
"Large Language models are",
"Barack Obama was",
"Decoding strategy is important because",
"A good recipe for Halloween is",
"Stanford is known for"
]
# Initialize accumulators for metrics
naive_entropy_totals = [0, 0, 0] # For n=1, 2, 3
naive_distinct_totals = [0, 0] # For n=1, 2
contrastive_entropy_totals = [0, 0, 0]
contrastive_distinct_totals = [0, 0]
for immediate in prompts:
naive_generated_text = sequential_sampling(immediate, max_length=50)[0]
for n in vary(1, 4):
naive_entropy_totals[n - 1] += ngram_entropy(naive_generated_text, n)
for n in vary(1, 3):
naive_distinct_totals[n - 1] += distinct_n(naive_generated_text, n)
contrastive_generated_text = contrastive_decoding(immediate, max_length=50)[0]
for n in vary(1, 4):
contrastive_entropy_totals[n - 1] += ngram_entropy(contrastive_generated_text, n)
for n in vary(1, 3):
contrastive_distinct_totals[n - 1] += distinct_n(contrastive_generated_text, n)
# Compute averages
naive_entropy_averages = [total / len(prompts) for total in naive_entropy_totals]
naive_distinct_averages = [total / len(prompts) for total in naive_distinct_totals]
contrastive_entropy_averages = [total / len(prompts) for total in contrastive_entropy_totals]
contrastive_distinct_averages = [total / len(prompts) for total in contrastive_distinct_totals]
# Show outcomes
print("Naive Sampling:")
for n in vary(1, 4):
print(f"Common Entropy (n={n}): {naive_entropy_averages[n - 1]}")
for n in vary(1, 3):
print(f"Common Distinct-{n}: {naive_distinct_averages[n - 1]}")
print("nContrastive Decoding:")
for n in vary(1, 4):
print(f"Common Entropy (n={n}): {contrastive_entropy_averages[n - 1]}")
for n in vary(1, 3):
print(f"Common Distinct-{n}: {contrastive_distinct_averages[n - 1]}")
The next outcomes present us that contrastive decoding outperforms naive sampling for these metrics.
Naive Sampling:
Common Entropy (n=1): 4.990499826537679
Common Entropy (n=2): 5.174765791328267
Common Entropy (n=3): 5.14373124004409
Common Distinct-1: 0.8949694135740648
Common Distinct-2: 0.9951219512195122Contrastive Decoding:
Common Entropy (n=1): 5.182773920916605
Common Entropy (n=2): 5.3495681172235665
Common Entropy (n=3): 5.313720275712986
Common Distinct-1: 0.9028425204970866
Common Distinct-2: 1.0
To guage speculative decoding, we will take a look at the common runtime for a set of prompts for various n values.
import time
import matplotlib.pyplot as plt# Parameters
n_tokens = vary(1, 11)
speculative_decoding_times = []
naive_decoding_times = []
prompts = [
"Large Language models are",
"Barack Obama was",
"Decoding strategy is important because",
"A good recipe for Halloween is",
"Stanford is known for"
]
# Loop by means of n_tokens values
for n in n_tokens:
avg_time_naive, avg_time_speculative = 0, 0
for immediate in prompts:
start_time = time.time()
_ = sequential_sampling(immediate, max_length=25)
avg_time_naive += (time.time() - start_time)
start_time = time.time()
_ = speculative_decoding(immediate, n_tokens=n, max_length=25)
avg_time_speculative += (time.time() - start_time)
naive_decoding_times.append(avg_time_naive / len(prompts))
speculative_decoding_times.append(avg_time_speculative / len(prompts))
avg_time_naive = sum(naive_decoding_times) / len(naive_decoding_times)
# Plotting the outcomes
plt.determine(figsize=(8, 6))
plt.bar(n_tokens, speculative_decoding_times, width=0.6, label='Speculative Decoding Time', alpha=0.7)
plt.axhline(y=avg_time_naive, shade='crimson', linestyle='--', label='Naive Decoding Time')
# Labels and title
plt.xlabel('n_tokens', fontsize=12)
plt.ylabel('Common Time (s)', fontsize=12)
plt.title('Speculative Decoding Runtime vs n_tokens', fontsize=14)
plt.legend()
plt.grid(axis='y', linestyle='--', alpha=0.7)
# Present the plot
plt.present()
plt.savefig("plot.png")
We will see that the common runtime for the naive decoding is way larger than for speculative decoding throughout n values.
Combining giant and small language fashions for decoding strikes a stability between high quality and effectivity. Whereas these approaches introduce further complexity in system design and useful resource administration, their advantages apply to conversational AI, real-time translation, and content material creation.
These approaches require cautious consideration of deployment constraints. For example, the extra reminiscence and compute calls for of operating twin fashions could restrict feasibility on edge gadgets, although this may be mitigated by means of methods like mannequin quantization.
Until in any other case famous, all photos are by the creator.