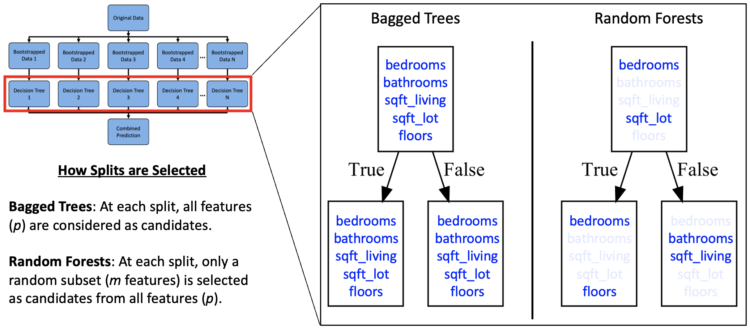
bushes are a well-liked supervised studying algorithm with advantages that embrace with the ability to be used for each regression and classification in addition to being straightforward to interpret. Nonetheless, determination bushes aren’t probably the most performant algorithm and are vulnerable to overfitting attributable to small variations within the coaching knowledge. This may end up in a very completely different tree. This is the reason folks typically flip to ensemble fashions like Bagged Bushes and Random Forests. These include a number of determination bushes educated on bootstrapped knowledge and aggregated to realize higher predictive efficiency than any single tree might supply. This tutorial consists of the next:
- What’s Bagging
- What Makes Random Forests Completely different
- Coaching and Tuning a Random Forest utilizing Scikit-Study
- Calculating and Deciphering Characteristic Significance
- Visualizing Particular person Resolution Bushes in a Random Forest
As all the time, the code used on this tutorial is out there on my GitHub. A video model of this tutorial can also be accessible on my YouTube channel for individuals who favor to observe alongside visually. With that, let’s get began!
What’s Bagging (Bootstrap Aggregating)

Random forests may be categorized as bagging algorithms (bootstrap aggregating). Bagging consists of two steps:
1.) Bootstrap sampling: Create a number of coaching units by randomly drawing samples with substitute from the unique dataset. These new coaching units, known as bootstrapped datasets, sometimes include the identical variety of rows as the unique dataset, however particular person rows might seem a number of instances or in no way. On common, every bootstrapped dataset incorporates about 63.2% of the distinctive rows from the unique knowledge. The remaining ~36.8% of rows are not noted and can be utilized for out-of-bag (OOB) analysis. For extra on this idea, see my sampling with and with out substitute weblog put up.
2.) Aggregating predictions: Every bootstrapped dataset is used to coach a unique determination tree mannequin. The ultimate prediction is made by combining the outputs of all particular person bushes. For classification, that is sometimes achieved by means of majority voting. For regression, predictions are averaged.
Coaching every tree on a unique bootstrapped pattern introduces variation throughout bushes. Whereas this doesn’t totally get rid of correlation—particularly when sure options dominate—it helps cut back overfitting when mixed with aggregation. Averaging the predictions of many such bushes reduces the general variance of the ensemble, enhancing generalization.
What Makes Random Forests Completely different

Suppose there’s a single sturdy characteristic in your dataset. In bagged bushes, every tree might repeatedly break up on that characteristic, resulting in correlated bushes and fewer profit from aggregation. Random Forests cut back this difficulty by introducing additional randomness. Particularly, they alter how splits are chosen throughout coaching:
1). Create N bootstrapped datasets. Word that whereas bootstrapping is often utilized in Random Forests, it isn’t strictly obligatory as a result of step 2 (random characteristic choice) introduces adequate range among the many bushes.
2). For every tree, at every node, a random subset of options is chosen as candidates, and the very best break up is chosen from that subset. In scikit-learn, that is managed by the max_features parameter, which defaults to 'sqrt' for classifiers and 1 for regressors (equal to bagged bushes).
3). Aggregating predictions: vote for classification and common for regression.
Word: Random Forests use sampling with substitute for bootstrapped datasets and sampling with out substitute for choosing a subset of options.

Out-of-Bag (OOB) Rating
As a result of ~36.8% of coaching knowledge is excluded from any given tree, you should utilize this holdout portion to judge that tree’s predictions. Scikit-learn permits this through the oob_score=True parameter, offering an environment friendly option to estimate generalization error. You’ll see this parameter used within the coaching instance later within the tutorial.
Coaching and Tuning a Random Forest in Scikit-Study
Random Forests stay a robust baseline for tabular knowledge because of their simplicity, interpretability, and talent to parallelize since every tree is educated independently. This part demonstrates find out how to load knowledge, carry out a practice check break up, practice a baseline mannequin, tune hyperparameters utilizing grid search, and consider the ultimate mannequin on the check set.
Step 1: Prepare a Baseline Mannequin
Earlier than tuning, it’s good follow to coach a baseline mannequin utilizing cheap defaults. This offers you an preliminary sense of efficiency and allows you to validate generalization utilizing the out-of-bag (OOB) rating, which is constructed into bagging-based fashions like Random Forests. This instance makes use of the Home Gross sales in King County dataset (CCO 1.0 Common License), which incorporates property gross sales from the Seattle space between Might 2014 and Might 2015. This strategy permits us to order the check set for last analysis after tuning.
Python"># Import libraries
# Some imports are solely used later within the tutorial
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# Dataset: Breast Most cancers Wisconsin (Diagnostic)
# Supply: UCI Machine Studying Repository
# License: CC BY 4.0
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import RandomForestRegressor
from sklearn.inspection import permutation_importance
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn import tree
# Load dataset
# Dataset: Home Gross sales in King County (Might 2014–Might 2015)
# License CC0 1.0 Common
url = 'https://uncooked.githubusercontent.com/mGalarnyk/Tutorial_Data/grasp/King_County/kingCountyHouseData.csv'
df = pd.read_csv(url)
columns = ['bedrooms',
'bathrooms',
'sqft_living',
'sqft_lot',
'floors',
'waterfront',
'view',
'condition',
'grade',
'sqft_above',
'sqft_basement',
'yr_built',
'yr_renovated',
'lat',
'long',
'sqft_living15',
'sqft_lot15',
'price']
df = df[columns]
# Outline options and goal
X = df.drop(columns='value')
y = df['price']
# Prepare/check break up
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# Prepare baseline Random Forest
reg = RandomForestRegressor(
n_estimators=100, # variety of bushes
max_features=1/3, # fraction of options thought-about at every break up
oob_score=True, # permits out-of-bag analysis
random_state=0
)
reg.match(X_train, y_train)
# Consider baseline efficiency utilizing OOB rating
print(f"Baseline OOB rating: {reg.oob_score_:.3f}")
Step 2: Tune Hyperparameters with Grid Search
Whereas the baseline mannequin provides a robust start line, efficiency can typically be improved by tuning key hyperparameters. Grid search cross-validation, as applied by GridSearchCV, systematically explores combos of hyperparameters and makes use of cross-validation to judge each, deciding on the configuration with the best validation efficiency.Essentially the most generally tuned hyperparameters embrace:
n_estimators: The variety of determination bushes within the forest. Extra bushes can enhance accuracy however enhance coaching time.max_features: The variety of options to contemplate when in search of the very best break up. Decrease values cut back correlation between bushes.max_depth: The utmost depth of every tree. Shallower bushes are quicker however might underfit.min_samples_split: The minimal variety of samples required to separate an inside node. Increased values can cut back overfitting.min_samples_leaf: The minimal variety of samples required to be at a leaf node. Helps management tree dimension.bootstrap: Whether or not bootstrap samples are used when constructing bushes. If False, the entire dataset is used.
param_grid = {
'n_estimators': [100],
'max_features': ['sqrt', 'log2', None],
'max_depth': [None, 5, 10, 20],
'min_samples_split': [2, 5],
'min_samples_leaf': [1, 2]
}
# Initialize mannequin
rf = RandomForestRegressor(random_state=0, oob_score=True)
grid_search = GridSearchCV(
estimator=rf,
param_grid=param_grid,
cv=5, # 5-fold cross-validation
scoring='r2', # analysis metric
n_jobs=-1 # use all accessible CPU cores
)
grid_search.match(X_train, y_train)
print(f"Finest parameters: {grid_search.best_params_}")
print(f"Finest R^2 rating: {grid_search.best_score_:.3f}")
Step 3: Consider Closing Mannequin on Take a look at Set
Now that we’ve chosen the best-performing mannequin primarily based on cross-validation, we will consider it on the held-out check set to estimate its generalization efficiency.
# Consider last mannequin on check set
best_model = grid_search.best_estimator_
print(f"Take a look at R^2 rating (last mannequin): {best_model.rating(X_test, y_test):.3f}")
Calculating Random Forest Characteristic Significance
One of many key benefits of Random Forests is their interpretability — one thing that enormous language fashions (LLMs) typically lack. Whereas LLMs are highly effective, they sometimes perform as black bins and may exhibit biases which can be troublesome to determine. In distinction, scikit-learn helps two foremost strategies for measuring characteristic significance in Random Forests: Imply Lower in Impurity and Permutation Significance.
1). Imply Lower in Impurity (MDI): Also called Gini significance, this technique calculates the entire discount in impurity introduced by every characteristic throughout all bushes. That is quick and constructed into the mannequin through reg.feature_importances_. Nonetheless, impurity-based characteristic importances may be deceptive, particularly for options with excessive cardinality (many distinctive values), as these options usually tend to be chosen just because they supply extra potential break up factors.
importances = reg.feature_importances_
feature_names = X.columns
sorted_idx = np.argsort(importances)[::-1]
for i in sorted_idx:
print(f"{feature_names[i]}: {importances[i]:.3f}")
2). Permutation Significance: This technique assesses the lower in mannequin efficiency when a single characteristic’s values are randomly shuffled. In contrast to MDI, it accounts for characteristic interactions and correlation. It’s extra dependable but additionally extra computationally costly.
# Carry out permutation significance on the check set
perm_importance = permutation_importance(reg, X_test, y_test, n_repeats=10, random_state=0)
sorted_idx = perm_importance.importances_mean.argsort()[::-1]
for i in sorted_idx:
print(f"{X.columns[i]}: {perm_importance.importances_mean[i]:.3f}")You will need to be aware that our geographic options lat and lengthy are additionally helpful for visualization because the plot beneath exhibits. It’s doubtless that firms like Zillow leverage location data extensively of their valuation fashions.

Visualizing Particular person Resolution Bushes in a Random Forest
A Random Forest consists of a number of determination bushes—one for every estimator specified through the n_estimators parameter. After coaching the mannequin, you possibly can entry these particular person bushes by means of the .estimators_ attribute. Visualizing a number of of those bushes might help illustrate how in a different way each splits the information attributable to bootstrapped coaching samples and random characteristic choice at every break up. Whereas the sooner instance used a RandomForestRegressor, right here we display this visualization utilizing a RandomForestClassifier educated on the Breast Most cancers Wisconsin dataset (CC BY 4.0 license) to spotlight Random Forests’ versatility for each regression and classification duties. This quick video demonstrates what 100 educated estimators from this dataset seem like.
Match a Random Forest Mannequin utilizing Scikit-Study
# Load the Breast Most cancers (Diagnostic) Dataset
knowledge = load_breast_cancer()
df = pd.DataFrame(knowledge.knowledge, columns=knowledge.feature_names)
df['target'] = knowledge.goal
# Organize Information into Options Matrix and Goal Vector
X = df.loc[:, df.columns != 'target']
y = df.loc[:, 'target'].values
# Cut up the information into coaching and testing units
X_train, X_test, Y_train, Y_test = train_test_split(X, y, random_state=0)
# Random Forests in `scikit-learn` (with N = 100)
rf = RandomForestClassifier(n_estimators=100,
random_state=0)
rf.match(X_train, Y_train)Plotting Particular person Estimators (determination bushes) from a Random Forest utilizing Matplotlib
Now you can view all the person bushes from the fitted mannequin.
rf.estimators_

Now you can visualize particular person bushes. The code beneath visualizes the primary determination tree.
fn=knowledge.feature_names
cn=knowledge.target_names
fig, axes = plt.subplots(nrows = 1,ncols = 1,figsize = (4,4), dpi=800)
tree.plot_tree(rf.estimators_[0],
feature_names = fn,
class_names=cn,
crammed = True);
fig.savefig('rf_individualtree.png')
Though plotting many bushes may be troublesome to interpret, you could want to discover the range throughout estimators. The next instance exhibits find out how to visualize the primary 5 determination bushes within the forest:
# This will not the easiest way to view every estimator as it's small
fig, axes = plt.subplots(nrows=1, ncols=5, figsize=(10, 2), dpi=3000)
for index in vary(5):
tree.plot_tree(rf.estimators_[index],
feature_names=fn,
class_names=cn,
crammed=True,
ax=axes[index])
axes[index].set_title(f'Estimator: {index}', fontsize=11)
fig.savefig('rf_5trees.png')
Conclusion
Random forests include a number of determination bushes educated on bootstrapped knowledge so as to obtain higher predictive efficiency than could possibly be obtained from any of the person determination bushes. If in case you have questions or ideas on the tutorial, be happy to succeed in out by means of YouTube or X.