Understanding Matrices | Half 2: Matrix-Matrix Multiplication

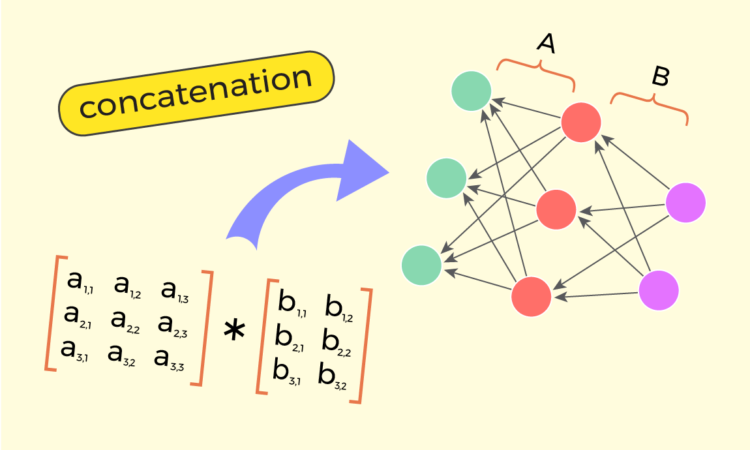
Within the first story [1] of this sequence, we’ve:

• Addressed multiplication of a matrix by a vector,
• Launched the idea of X-diagram for a given matrix,
• Noticed habits of a number of particular matrices, when being multiplied by a vector.

Within the present 2nd story, we’ll grasp the bodily that means of matrix-matrix multiplication, perceive why multiplication just isn’t a symmetrical operation (i.e., why “A*B ≠ B*A“), and at last, we’ll see how a number of particular matrices behave when being multiplied over one another.

So let’s begin, and we’ll do it by recalling the definitions that I take advantage of all through this sequence:

• Matrices are denoted with uppercase (like ‘A‘ and ‘B‘), whereas vectors and scalars are denoted with lowercase (like ‘x‘, ‘y‘ or ‘m‘, ‘n‘).
• |x| – is the size of vector ‘x‘,
• rows(A) – variety of rows of matrix ‘A‘,
• columns(A) – variety of columns of matrix ‘A‘.

The idea of multiplying matrices

Multiplication of two matrices “A” and “B” might be the most typical operation in matrix evaluation. A identified truth is that “A” and “B” will be multiplied provided that “columns(A) = rows(B)”. On the identical time, “A” can have any variety of rows, and “B” can have any variety of columns. Cells of the product matrix “C = A*B” are calculated by the next components:

[
begin{equation*}
c_{i,j} = sum_{k=1}^{p} a_{i,k}*b_{k,j}
end{equation*}
]

the place “p = columns(A) = rows(B)”. The consequence matrix “C” can have the scale:

rows(C) = rows(A),
columns(C) = columns(B).

Performing upon the multiplication components, when calculating “A*B” we should always scan i-th row of “A” in parallel to scanning j-th column of “B“, and after summing up all of the merchandise “a_i,okay*b_okay,j” we can have the worth of “c_i,j“.

One other well-known truth is that matrix multiplication just isn’t a symmetrical operation, i.e., “A*B ≠ B*A“. With out going into particulars, we are able to already see that when multiplying 2 rectangular matrices:

For newbies, the truth that matrix multiplication just isn’t a symmetrical operation typically appears unusual, as multiplication outlined for nearly another object is a symmetrical operation. One other truth that’s typically unclear is why matrix multiplication is carried out by such an odd components.

On this story, I’m going to offer my solutions to each of those questions, and never solely to them…

Derivation of the matrices multiplication components

Multiplying “A*B” ought to produce such a matrix ‘C‘, that:

y = C*x = (A*B)*x = A*(B*x).

In different phrases, multiplying any vector ‘x‘ by the product matrix “C=A*B” ought to end in the identical vector ‘y‘, which we’ll obtain if at first multiplying ‘B‘ by ‘x‘, after which multiplying ‘A‘ by that intermediate consequence.

This already explains why in “C=A*B“, the situation that “columns(A) = rows(B)” must be saved. That’s due to the size of the intermediate vector. Let’s denote it as ‘t‘:

t = B*x,
y = C*x = (A*B)*x = A*(B*x) = A*t.

Clearly, as “t = B*x“, we’ll obtain a vector ‘t‘ of size “|t| = rows(B)”. However later, matrix ‘A‘ goes to be multiplied by ‘t‘, which requires ‘t‘ to have the size “|t| = columns(A)”. From these 2 information, we are able to already work out that:

rows(B) = |t| = columns(A), or
rows(B) = columns(A).

Within the first story [1] of this sequence, we’ve realized the “X-way interpretation” of matrix-vector multiplication “A*x“. Contemplating that for “y = (A*B)x“, vector ‘x‘ goes at first by way of the transformation of matrix ‘B‘, after which it continues by way of the transformation of matrix ‘A‘, we are able to broaden the idea of “X-way interpretation” and current matrix-matrix multiplication “A*B” as 2 adjoining X-diagrams:

Now, what ought to a sure cell “c_i,j” of matrix ‘C‘ be equal to? From half 1 – “matrix-vector multiplication” [1], we do not forget that the bodily that means of “c_i,j” is – how a lot the enter worth ‘x_j‘ impacts the output worth ‘y_i‘. Contemplating the image above, let’s see how some enter worth ‘x_j‘ can have an effect on another output worth ‘y_i‘. It will possibly have an effect on by way of the intermediate worth ‘t₁‘, i.e., by way of arrows “a_i,1” and “b_1,j“. Additionally, the love can happen by way of the intermediate worth ‘t₂‘, i.e., by way of arrows “a_i,2” and “b_2,j“. Typically, the love of ‘x_j‘ on ‘y_i‘ can happen by way of any worth ‘t_okay‘ of the intermediate vector ‘t‘, i.e., by way of arrows “a_i,okay” and “b_okay,j“.

So there are ‘p‘ attainable methods by which the worth ‘x_j‘ influences ‘y_i‘, the place ‘p‘ is the size of the intermediate vector: “p = |t| = |B*x|”. The influences are:

[begin{equation*}
begin{matrix}
a_{i,1}*b_{1,j},
a_{i,2}*b_{2,j},
a_{i,3}*b_{3,j},
dots
a_{i,p}*b_{p,j}
end{matrix}
end{equation*}]

All these ‘p‘ influences are unbiased of one another, which is why within the components of matrices multiplication they take part as a sum:

[begin{equation*}
c_{i,j} =
a_{i,1}*b_{1,j} + a_{i,2}*b_{2,j} + dots + a_{i,p}*b_{p,j} =
sum_{k=1}^{p} a_{i,k}*b_{k,j}
end{equation*}]

That is my visible clarification of the matrix-matrix multiplication components. By the way in which, decoding “A*B” as a concatenation of X-diagrams of “A” and “B” explicitly reveals why the situation “columns(A) = rows(B)” must be held. That’s easy, as a result of in any other case it won’t be attainable to concatenate the 2 X-diagrams:

Why is it that “A*B ≠ B*A”

Decoding matrix multiplication “A*B” as a concatenation of X-diagrams of “A” and “B” additionally explains why multiplication just isn’t symmetrical for matrices, i.e., why “A*B ≠ B*A“. Let me present that on two sure matrices:

[begin{equation*}
A =
begin{bmatrix}
0 & 0 & 0 & 0
0 & 0 & 0 & 0
a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4}
a_{4,1} & a_{4,2} & a_{4,3} & a_{4,4}
end{bmatrix}
, B =
begin{bmatrix}
b_{1,1} & b_{1,2} & 0 & 0
b_{2,1} & b_{2,2} & 0 & 0
b_{3,1} & b_{3,2} & 0 & 0
b_{4,1} & b_{4,2} & 0 & 0
end{bmatrix}
end{equation*}]

Right here, matrix ‘A‘ has its higher half crammed with zeroes, whereas ‘B‘ has zeroes on its proper half. Corresponding X-diagrams are:

What is going to occur if making an attempt to multiply “A*B“? Then A’s X-diagram must be positioned to the left of B’s X-diagram.

Having such a placement, we see that enter values ‘x₁‘ and ‘x₂‘ can have an effect on each output values ‘y₃‘ and ‘y₄‘. Notably, which means that the product matrix “A*B” is non-zero.

[
begin{equation*}
A*B =
begin{bmatrix}
0 & 0 & 0 & 0
0 & 0 & 0 & 0
c_{3,1} & c_{3,2} & 0 & 0
c_{4,1} & c_{4,2} & 0 & 0
end{bmatrix}
end{equation*}
]

Now, what is going to occur if we attempt to multiply these two matrices within the reverse order? For presenting the product “B*A“, B’s X-diagram must be drawn to the left of A’s diagram:

We see that now there isn’t any related path, by which any enter worth “x_j” can have an effect on any output worth “y_i“. In different phrases, within the product matrix “B*A” there isn’t any affection in any respect, and it’s really a zero-matrix.

[begin{equation*}
B*A =
begin{bmatrix}
0 & 0 & 0 & 0
0 & 0 & 0 & 0
0 & 0 & 0 & 0
0 & 0 & 0 & 0
end{bmatrix}
end{equation*}]

This instance clearly illustrates why order is necessary for matrix-matrix multiplication. After all, many different examples can be discovered.

Multiplying chain of matrices

X-diagrams can be concatenated after we multiply 3 or extra matrices. For instance, for the case of:

G = A*B*C,

we are able to draw the concatenation within the following means:

Right here we now have 2 intermediate vectors:

t = C*x, and
s = (B*C)*x = B*(C*x) = B*t

whereas the consequence vector is:

y = (A*B*C)*x = A*(B*(C*x)) = A*(B*t) = A*s.

The variety of attainable methods by which some enter worth “x_j” can have an effect on some output worth “y_i” grows right here by an order of magnitude.

Extra exactly, the affect of sure “x_j” over “y_i” can come by way of any merchandise of the primary intermediate stack “t“, and any merchandise of the second intermediate stack “s“. So the variety of methods of affect turns into “|t|*|s|”, and the components for “g_i,j” turns into:

[begin{equation*}
g_{i,j} = sum_{v=1}^ sum_{u=1}^t a_{i,v}*b_{v,u}*c_{u,j}
end{equation*}]

Multiplying matrices of particular varieties

We are able to already visually interpret matrix-matrix multiplication. Within the first story of this sequence [1], we additionally realized about a number of particular varieties of matrices – the size matrix, shift matrix, permutation matrix, and others. So let’s check out how multiplication works for these varieties of matrices.

Multiplication of scale matrices

A scale matrix has non-zero values solely on its diagonal:

From idea, we all know that multiplying two scale matrices ends in one other scale matrix. Why is it that means? Let’s concatenate X-diagrams of two scale matrices:

The concatenation X-diagram clearly reveals that any enter merchandise “x_i” can nonetheless have an effect on solely the corresponding output merchandise “y_i“. It has no means of influencing another output merchandise. Subsequently, the consequence construction behaves the identical means as another scale matrix.

Multiplication of shift matrices

A shift matrix is one which, when multiplied over some enter vector ‘x‘, shifts upwards or downwards values of ‘x‘ by some ‘okay‘ positions, filling the emptied slots with zeroes. To attain that, a shift matrix ‘V‘ will need to have 1(s) on a line parallel to its major diagonal, and 0(s) in any respect different cells.

The speculation says that multiplying 2 shift matrices ‘V1‘ and ‘V2‘ ends in one other shift matrix. Interpretation with X-diagrams provides a transparent clarification of that. Multiplying the shift matrices ‘V1‘ and ‘V2‘ corresponds to concatenating their X-diagrams:

We see that if shift matrix ‘V1‘ shifts values of its enter vector by ‘k1‘ positions upwards, and shift matrix ‘V2‘ shifts values of the enter vector by ‘k2‘ positions upwards, then the outcomes matrix “V3 = V1*V2” will shift values of the enter vector by ‘k1+k2‘ positions upwards, which signifies that “V3” can be a shift matrix.

Multiplication of permutation matrices

A permutation matrix is one which, when multiplied by an enter vector ‘x‘, rearranges the order of values in ‘x‘. To behave like that, the NxN-sized permutation matrix ‘P‘ should fulfill the next standards:

• it ought to have N 1(s),
• no two 1(s) must be on the identical row or the identical column,
• all remaining cells must be 0(s).

Upon idea, multiplying 2 permutation matrices ‘P1‘ and ‘P2‘ ends in one other permutation matrix ‘P3‘. Whereas the explanation for this may not be clear sufficient if matrix multiplication within the strange means (as scanning rows of ‘P1‘ and columns of ‘P2‘), it turns into a lot clearer if it by way of the interpretation of X-diagrams. Multiplying “P1*P2” is identical as concatenating X-diagrams of ‘P1‘ and ‘P2‘.

We see that each enter worth ‘x_j‘ of the appropriate stack nonetheless has just one path for reaching another place ‘y_i‘ on the left stack. So “P1*P2” nonetheless acts as a rearrangement of all values of the enter vector ‘x‘, in different phrases, “P1*P2” can be a permutation matrix.

Multiplication of triangular matrices

A triangular matrix has all zeroes both above or beneath its major diagonal. Right here, let’s consider upper-triangular matrices, the place zeroes are beneath the principle diagonal. The case of lower-triangular matrices is analogous.

The truth that non-zero values of ‘B‘ are both on its major diagonal or above, makes all of the arrows of its X-diagram both horizontal or directed upwards. This, in flip, signifies that any enter worth ‘x_j‘ of the appropriate stack can have an effect on solely these output values ‘y_i‘ of the left stack, which have a lesser or equal index (i.e., “i ≤ j“). That is likely one of the properties of an upper-triangular matrix.

In response to idea, multiplying two upper-triangular matrices ends in one other upper-triangular matrix. And right here too, interpretation with X-diagrams supplies a transparent clarification of that truth. Multiplying two upper-triangular matrices ‘A‘ and ‘B‘ is identical as concatenating their X-diagrams:

We see that placing two X-diagrams of triangular matrices ‘A‘ and ‘B‘ close to one another ends in such a diagram, the place each enter worth ‘x_j‘ of the appropriate stack nonetheless can have an effect on solely these output values ‘y_i‘ of the left stack, that are both on its stage or above it (in different phrases, “i ≤ j“). Because of this the product “A*B” additionally behaves like an upper-triangular matrix; thus, it will need to have zeroes beneath its major diagonal.

Conclusion

Within the present 2nd story of this sequence, we noticed how matrix-matrix multiplication will be introduced visually, with the assistance of so-called “X-diagrams”. Now we have realized that doing multiplication “C = A*B” is identical as concatenating X-diagrams of these two matrices. This methodology clearly illustrates numerous properties of matrix multiplications, like why it’s not a symmetrical operation (“A*B ≠ B*A“), in addition to explains the components:

[begin{equation*}
c_{i,j} = sum_{k=1}^{p} a_{i,k}*b_{k,j}
end{equation*}]

Now we have additionally noticed why multiplication behaves in sure methods when operands are matrices of particular varieties (scale, shift, permutation, and triangular matrices).

I hope you loved studying this story!

Within the coming story, we’ll handle how matrix transposition “A^T” will be interpreted with X-diagrams, and what we are able to acquire from such interpretation, so subscribe to my web page to not miss the updates!

My gratitude to:
– Roza Galstyan, for cautious evaluation of the draft ( https://www.linkedin.com/in/roza-galstyan-a54a8b352 )
– Asya Papyan, for the exact design of all of the used illustrations ( https://www.behance.internet/asyapapyan ).

If you happen to loved studying this story, be at liberty to comply with me on LinkedIn, the place, amongst different issues, I may also put up updates ( https://www.linkedin.com/in/tigran-hayrapetyan-cs/ ).

All used photos, except in any other case famous, are designed by request of the writer.

References

[1] – Understanding matrices | Half 1: matrix-vector multiplication : https://towardsdatascience.com/understanding-matrices-part-1-matrix-vector-multiplication/