0.
You’re actually already conversant in spherical or 360 photos. They’re utilized in Google Avenue View or in digital home excursions to offer you an immersive feeling by letting you go searching in any route.
Since such photos lie on the unit sphere, storing them in reminiscence as flat photos could be tough. In observe, we normally retailer them as flat arrays utilizing one of many two following codecs:
- Cubemap (6 photos): every picture corresponds to the face of a dice onto which the unit sphere has been projected.
- Equirectangular picture: much like a planisphere map of the Earth. The south and north poles of the unit sphere are stretched to flatten the picture onto a daily grid. In contrast to the cubemap, the picture is saved as a single picture which simplifies the boundary dealing with throughout picture processing. However this method introduces vital distortion.


In a earlier article (Understanding 360 photos), I defined the maths behind the conversion between these two codecs. On this article we’ll focus as an alternative solely on the equirectangular format and examine the maths behind modifying the digicam pose of an equirectangular picture.
It’s a terrific alternative to raised perceive spherical coordinates, rotation matrices and picture remapping!
The pictures beneath illustrate the type of rework we’d like to use.
“What would my 360 picture appear like if it had been tilted 20° downwards?”

“What would my 360 picture appear like if it had been shifted 45° to the best?”

“What would my 360 picture appear like if it had been shifted 45° to the best and tilted 20° downwards?”

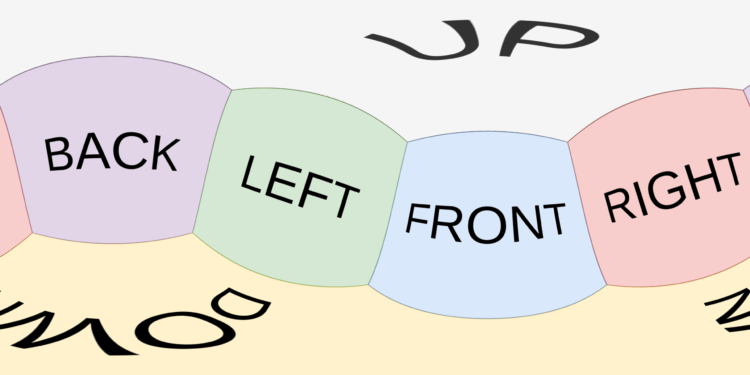
N.B. Probably the most extensively used picture coordinates system is to have the vertical Y axis pointing downwards within the picture and the horizontal X axis pointing to the best. Thus, I discover it extra intuitive {that a} optimistic horizontal Δθ shift strikes the picture to the best, whereas a destructive Δθ strikes it to the left. Nevertheless this counterintuitively implies that transferring the picture to the best corresponds to wanting left within the precise scene! Equally a optimistic vertical Δφ tilt strikes the picture downwards. The selection of conference is bigoted, it doesn’t actually matter.

1. Spherical Digicam Mannequin
Spherical coordinates
On a planisphere map of the Earth, horizontal traces correspond to latitudes whereas vertical traces correspond to longitudes.
When changing from cartesian to spherical coordinates, some extent M within the scene is absolutely described by its radius r and its two angles θ and φ. These angles permit us to unwrap the sphere into an equirectangular picture, the place θ serves because the longitude and φ because the latitude.

I’ve arbitrarily chosen to make use of the Right_Down_Front XYZ digicam conference (See my earlier article about digicam poses) and to have θ=φ=0 in entrance of us. Be at liberty to make use of one other conference. You get the identical picture on the finish anyway. I simply discover it extra handy.
The picture beneath illustrates the conference we’re utilizing, with θ various horizontally on the equirectangular picture from -π on the left, 0 on the middle and +π on the best. Word that the left and proper edges of the picture easily lengthen one another. As for φ, the north pole is at -π/2 and the south pole is at π/2.

Mapping to pixel coordinates is then simply an affine rework.

Rotation Matrices
When working with 3D rotations it may shortly get messy with out utilizing matrix kind. Rotation matrices present a handy option to categorical rotations as plain matrix-vector multiplications.
In our Right_Down_Front XYZ digicam conference (arbitrarily chosen), the rotation of angle φ across the X axis is described by the matrix beneath.

As you may see, this matrix leaves the X-axis unchanged because it’s its rotation axis.
Having cosines alongside the diagonal is sensible as a result of φ=0 should yield the identification matrix.
As for the signal earlier than the sines, I discover it useful to check with the spherical coordinates diagram above and take into consideration what would occur for a tiny optimistic φ. The purpose immediately in entrance of the digicam is (0,0,1), i.e. the tip of the entrance axis Z, and can thus be rotated into the final column of Rφ: (0, sinφ, cosφ). This offers us a vector near Z but additionally with a tiny optimistic element alongside the Y axis, precisely as anticipated!
Equally, we’ve the matrix describing the rotation of angle θ across the Y axis.

Conversion between cartesian and spherical coordinates
The purpose M with spherical coordinates (φ,θ) could be transformed to 3D cartesian coordinates p by ranging from the purpose (0,0,1) in entrance of the digicam, tilting it by φ across the X axis and at last panning it by θ across the Y axis.

The equations beneath derive the cartesian coordinates by successively making use of the rotation matrices on (0,0,1). The radius r has been omitted since we’re solely within the unit sphere.

To recuperate the spherical angles (φ,θ) we merely have to use the inverse trigonometric capabilities to the parts of p. Word that since φ lies in [-π/2,π/2] we all know that the issue cosφ is assured to stay optimistic, which permits us to securely apply arctan2.


2. Tilt/Pan 360 picture
Picture remapping
Our purpose is to rework an equirectangular picture into one other equirectangular picture, that mimics a (Δφ, Δθ) angular shift. In Understanding 360 photos I defined learn how to rework between equirectangular photos and cubemaps. Essentially it’s the identical course of: a sampling activity the place we apply a rework to current pixels to generate new pixels.
Because the rework can produce floating-point coordinates we’ve to make use of interpolation somewhat than simply transferring integer pixels.
It could sound counter-intuitive, however when remapping a picture we really want the reverse rework and never the rework itself. The determinant of the Jacobian of the rework defines how native density adjustments, which suggests there gained’t at all times be a one-to-one correspondence between enter and output pixels. If we had been to use the rework to every of the enter pixels to populate the brand new picture we may find yourself with enormous holes within the remodeled picture due to density variations.
Thus we have to outline the reverse rework, in order that we are able to iterate over every output pixel coordinates, map them again to the enter picture and interpolate its colour from the neighboring pixels.
Transition Matrix
We now have two 3D coordinates techniques:
- Body 0: Enter 360 picture
- Body 1: Output 360 picture remodeled by (Δφ, Δθ)
Every body can outline regionally its personal spherical angles.

We’re now on the lookout for the three×3 transition matrix between each frames.
The transition is outlined by the truth that we would like the middle of the enter picture 0 to be mapped to the purpose at (Δφ, Δθ) within the output picture 1.

It seems that it’s exactly what we already do within the spherical coordinates system: mapping the purpose at (0,0,1) to given spherical angles. Thus we find yourself with the next rework.

The reverse rework is then:

Warning: Rotation matrices usually don’t commute when their rotation axes differ. Order issues!
This immediately provides us the pose of the remodeled digicam. In truth, you may change p1 by any base axis of body 1 (1,0,0), (0,1,0) and (0,0,1) and take a look at the place it lands in body 0.
Thus, the digicam is first panned by -Δθ after which tilted by -Δφ. That is precisely what you’d do intuitively together with your digicam: orient your self in direction of the goal after which alter the lean. Reversing the order would end in a skewed or rolled digicam orientation.
Reverse rework
Let’s develop the matrix kind to finish up with a clear closed-form expression for the reverse rework yielding angles 0 from angles 1.

First we substitute p1 with its definition to make φ1 and θ1 seem.

It seems that each rotation matrices across the Y axis find yourself side-by-side and could be merged right into a single rotation matrix of angle θ1-Δθ.
The appropriate a part of the equation corresponds to a spherical level of coordinates (φ1, θ1-Δθ). We substitute it by its express kind.

We then substitute the remaining rotation matrix with its express kind and carry out the multiplication.

We lastly use inverse trigonometric capabilities to retrieve (φ0,θ0).

Nice! We now know the place to interpolate throughout the enter picture.
Code
The code beneath hundreds a spherical picture, selects arbitrary rotation angles (Δφ,Δθ), computes the reverse rework maps and at last applies them utilizing cv2.remap to get the output remodeled picture.
N.B. is meant for pedagogical functions. There may be nonetheless room for efficiency optimization!
Digicam Pan solely
What if Δφ=0 and the rework is a pure pan?
When Δφ=0 the rotation matrix turns into the identification and the expression of p0 simplifies to its canonical kind in spherical coordinates (φ1, θ1-Δθ).

The rework is easy and is only a plain subtraction on the θ angle. We’re principally merely rolling the picture horizontally utilizing a floating-point Δθ shift.

Digicam Tilt solely
What if Δθ=0 and the rework is a pure tilt?
When Δθ=0 the rotation matrix turns into the identification. However sadly it doesn’t change something, we’ve simply changed θ1-Δθ by θ1 within the equation, that’s it.


3. Habits at Picture Boundaries
Introduction
It might be attention-grabbing to see how factors at boundaries of the enter 360 picture are affected by the rework.
As an illustration, the south pole corresponds to φ0=π/2, which considerably simplifies the equations with cos(φ0)=0 and sin(φ0)=1. And we additionally know that the worth of θ0 doesn’t matter since every pole is decreased to a single level.
Sadly, substituting φ0=π/2 into the ultimate reverse rework system derived above provides us a clearly non-trivial equation to resolve for (φ1,θ1).

Basic mistake! As a substitute of utilizing the reverse rework system, it could be a lot easier to make use of the ahead rework. Let’s derive it.
Direct Remodel
In contrast to the reverse rework we are able to’t merge rotation matrices as a result of pan and tilt rotations strictly alternate.

Let’s use the express type of p0 and the rotations matrices Δθ and Δφ. Since factors (φ0,θ0) on the picture boundary drastically simplify the equations due to their handy cos(φ0) and sin(φ0) values, I’ve chosen to compute solely the product of RΔφ and RΔθ to maintain substitutions for trivial p0 values easy.

North/South Poles
The south pole is outlined by φ0=π/2. We now have cos(φ0)=0 and sin(φ0)=1 which simplifies the product into merely protecting the second column of the rotation matrix.

As anticipated θ0 doesn’t seem within the expression. Though the poles are infinitely stretched on the high/backside of the spherical picture they’re nonetheless single factors in 3D area.

Contemplating Δφ in [-π,π], we are able to change φ1 by π/2-|Δφ|.

As for θ1 it would depend upon the signal of sinΔφ. Word that on [-π,π] sinΔφ and Δφ have the identical signal. Lastly, we get:

When Δφ<0, the picture tilts downwards and the digicam begins wanting upwards. Consequently the south pole seems in entrance of the digicam at θ1=Δθ. Nevertheless, when Δφ>0 the digicam begins wanting downwards and the south pole strikes to the again, which explains the θ1=Δθ+π.
The mathematics for the north pole could be very comparable, we get:

In actual life 360 photos the south pole is simple to identify as a result of it corresponds to the tripod. To make this clearer, I’ve added within the determine beneath a inexperienced band on the backside of the enter 360 picture to mark the south pole and a magenta band on the high to spotlight the north pole. The left column corresponds to destructive Δφ angles, whereas the best column corresponds to optimistic Δφ angles.

Left/Proper Edge
The left and proper fringe of the 360 picture coincide and correspond to θ0=±π, which suggests cosθ0=-1 and sinθ0=0.
Figuring out the cosine distinction identification helps simplifying the equations.

The inverse trigonometric capabilities give us:

So long as you stay on [-π/2,π/2], arcsin(sinx) is the identification perform. However past this vary, the perform turns right into a periodic triangular wave.

As for θ1 it is going to be both Δθ or Δθ+π relying on the signal of cos(φ0-Δφ).
It’s truly actually intuitive: the back and front edges are simply the connections between the north and south poles. Because the poles translate alongside Δθ and Δθ+π the entrance/again edges merely comply with them alongside these two vertical tracks.
Within the photos beneath I’ve highlighted the entrance edge in cyan and the again edge in pink. Like earlier than, the left column corresponds to destructive Δφ angles, whereas the best column corresponds to optimistic Δφ angles.


Conclusion
I hope you loved as a lot as I did completely investigating what it truly means to pan or tilt a spherical picture!
The mathematics can get a bit verbose at occasions, however the matrix kind helps loads protecting issues tidy and on the finish the ultimate formulation aren’t that lengthy.
Ultimately it’s actually satisfying to use the rework onto the picture with only a dozen of traces of code.
When you really perceive how picture remapping works you may simply use it for lots of functions: changing between cubemaps and spherical photos, undistorting photos, stitching panoramas…