Survival Evaluation When No One Dies: A Worth-Based mostly Strategy

is a statistical strategy used to reply the query: “How lengthy will one thing final?” That “one thing” may vary from a affected person’s lifespan to the sturdiness of a machine part or the period of a consumer’s subscription.

Probably the most broadly used instruments on this space is the Kaplan-Meier estimator.

Born on the planet of biology, Kaplan-Meier made its debut monitoring life and dying. However like all true movie star algorithm, it didn’t keep in its lane. Lately, it’s exhibiting up in enterprise dashboards, advertising groups, and churn analyses in all places.

However right here’s the catch: enterprise isn’t biology. It’s messy, unpredictable, and stuffed with plot twists. For this reason there are a few points that make our lives harder after we attempt to use survival evaluation within the enterprise world.

To begin with, we’re sometimes not simply concerned about whether or not a buyer has “survived” (no matter survival may imply on this context), however slightly in how a lot of that particular person’s financial worth has survived.

Secondly, opposite to biology, it’s very attainable for patrons to “die” and “resuscitate” a number of occasions (consider whenever you unsubscribe/resubscribe to an internet service).

On this article, we’ll see find out how to lengthen the classical Kaplan-Meier strategy in order that it higher fits our wants: modeling a steady (financial) worth as an alternative of a binary one (life/dying) and permitting “resurrections”.

A refresher on the Kaplan-Meier estimator

Let’s pause and rewind for a second. Earlier than we begin customizing Kaplan-Meier to suit our enterprise wants, we want a fast refresher on how the traditional model works.

Suppose you had 3 topics (let’s say lab mice) and also you gave them a drugs that you must check. The drugs was given at completely different moments in time: topic a obtained it in January, topic b in April, and topic c in Might.

Then, you measure how lengthy they survive. Topic a died after 6 months, topic c after 4 months, and topic b remains to be alive on the time of the evaluation (November).

Graphically, we will symbolize the three topics as follows:

Now, even when we needed to measure a easy metric, like common survival, we’d face an issue. Actually, we don’t know the way lengthy topic b will survive, as it’s nonetheless alive at present.

This can be a classical downside in statistics, and it’s referred to as “proper censoring“.

Proper censoring is stats-speak for “we don’t know what occurred after a sure level” and it’s a giant deal in survival evaluation. So large that it led to the event of probably the most iconic estimators in statistical historical past: the Kaplan-Meier estimator, named after the duo who launched it again within the Nineteen Fifties.

So, how does Kaplan-Meier deal with our downside?

First, we align the clocks. Even when our mice had been handled at completely different occasions, what issues is time since therapy. So we reset the x-axis to zero for everybody — day zero is the day they bought the drug.

Now that we’re all on the identical timeline, we need to construct one thing helpful: an mixture survival curve. This curve tells us the chance {that a} typical mouse in our group will survive no less than x months post-treatment.

Let’s observe the logic collectively.

• As much as time 3? Everybody’s nonetheless alive. So survival = 100%. Simple.
• At time 4, mouse c dies. Which means that out of the three mice, solely 2 of them survived after time 4. That offers us a survival price of 67% at time 4.
• Then at time 6, mouse a checks out. Of the two mice that had made it to time 6, only one survived, so the survival price from time 5 to six is 50%. Multiply that by the earlier 67%, and we get 33% survival as much as time 6.
• After time 7 we don’t produce other topics which can be noticed alive, so the curve has to cease right here.

Let’s plot these outcomes:

Since code is usually simpler to grasp than phrases, let’s translate this to Python. Now we have the next variables:

• kaplan_meier, an array containing the Kaplan-Meier estimates for every time limit, e.g. the chance of survival as much as time t.
• obs_t, an array that tells us whether or not a person is noticed (e.g., not right-censored) at time t.
• surv_t, boolean array that tells us whether or not every particular person is alive at time t.
• surv_t_minus_1, boolean array that tells us whether or not every particular person is alive at time t-1.

All we have now to do is to take all of the people noticed at t, compute their survival price from t-1 to t (survival_rate_t), and multiply it by the survival price as much as time t-1 (km[t-1]) to acquire the survival price as much as time t (km[t]). In different phrases,

survival_rate_t = surv_t[obs_t].sum() / surv_t_minus_1[obs_t].sum()

kaplan_meier[t] = kaplan_meier[t-1] * survival_rate_t

the place, after all, the place to begin is kaplan_meier[0] = 1.

In the event you don’t need to code this from scratch, the Kaplan-Meier algorithm is out there within the Python library lifelines, and it may be used as follows:

from lifelines import KaplanMeierFitter

KaplanMeierFitter().match(
    durations=[6,7,4],
    event_observed=[1,0,1],
).survival_function_["KM_estimate"]

In the event you use this code, you’ll get hold of the identical end result we have now obtained manually with the earlier snippet.

To date, we’ve been hanging out within the land of mice, medication, and mortality. Not precisely your common quarterly KPI assessment, proper? So, how is this handy in enterprise?

Shifting to a enterprise setting

To date, we’ve handled “dying” as if it’s apparent. In Kaplan-Meier land, somebody both lives or dies, and we will simply log the time of dying. However now let’s stir in some real-world enterprise messiness.

What even is “dying” in a enterprise context?

It seems it’s not simple to reply this query, no less than for a few causes:

1. “Demise” is just not simple to outline. Let’s say you’re working at an e-commerce firm. You need to know when a consumer has “died”. Do you have to depend them as useless after they delete their account? That’s simple to trace… however too uncommon to be helpful. What if they simply begin procuring much less? However how a lot much less is useless? Per week of silence? A month? Two? You see the issue. The definition of “dying” is unfair, and relying on the place you draw the road, your evaluation may inform wildly completely different tales.
2. “Demise” is just not everlasting. Kaplan-Meier has been conceived for organic functions through which as soon as a person is useless there is no such thing as a return. However in enterprise functions, resurrection is just not solely attainable however fairly frequent. Think about a streaming service for which individuals pay a month-to-month subscription. It’s simple to outline “dying” on this case: it’s when customers cancel their subscriptions. Nevertheless, it’s fairly frequent that, a while after cancelling, they re-subscribe.

So how does all this play out in information?

Let’s stroll by a toy instance. Say we have now a consumer on our e-commerce platform. Over the previous 10 months, right here’s how a lot they’ve spent:

To squeeze this into the Kaplan-Meier framework, we have to translate that spending conduct right into a life-or-death determination.

So we make a rule: if a consumer stops spending for two consecutive months, we declare them “inactive”.

Graphically, this rule seems to be like the next:

For the reason that consumer spent $0 for 2 months in a row (month 4 and 5) we’ll contemplate this consumer inactive ranging from month 4 on. And we’ll try this regardless of the consumer began spending once more in month 7. It’s because, in Kaplan-Meier, resurrections are assumed to be unattainable.

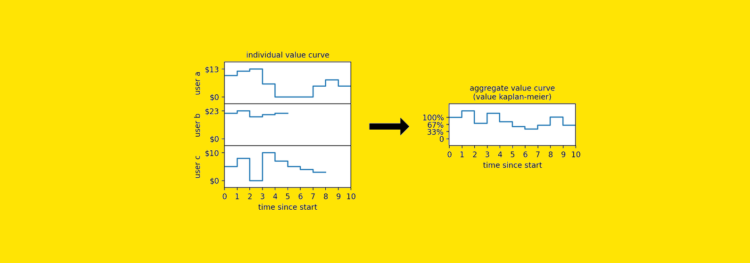
Now let’s add two extra customers to our instance. Since we have now determined a rule to show their worth curve right into a survival curve, we will additionally compute the Kaplan-Meier survival curve:

By now, you’ve in all probability seen how a lot nuance (and information) we’ve thrown away simply to make this work. Consumer a got here again from the useless — however we ignored that. Consumer c‘s spending dropped considerably — however Kaplan-Meier doesn’t care, as a result of all it sees is 1s and 0s. We pressured a steady worth (spending) right into a binary field (alive/useless), and alongside the way in which, we misplaced an entire lot of data.

So the query is: can we lengthen Kaplan-Meier in a approach that:

• retains the unique, steady information intact,
• avoids arbitrary binary cutoffs,
• permits for resurrections?

Sure, we will. Within the subsequent part, I’ll present you ways.

Introducing “Worth Kaplan-Meier”

Let’s begin with the easy Kaplan-Meier components we have now seen earlier than.

# kaplan_meier: array containing the Kaplan-Meier estimates,
#               e.g. the chance of survival as much as time t
# obs_t: array, whether or not a topic has been noticed at time t
# surv_t: array, whether or not a topic was alive at time t
# surv_t_minus_1: array, whether or not a topic was alive at time t−1

survival_rate_t = surv_t[obs_t].sum() / surv_t_minus_1[obs_t].sum()

kaplan_meier[t] = kaplan_meier[t-1] * survival_rate_t

The primary change we have to make is to interchange surv_t and surv_t_minus_1, that are boolean arrays that inform us whether or not a topic is alive (1) or useless (0) with arrays that inform us the (financial) worth of every topic at a given time. For this objective, we will use two arrays named val_t and val_t_minus_1.

However this isn’t sufficient, as a result of since we’re coping with steady worth, each consumer is on a unique scale and so, assuming that we need to weigh them equally, we have to rescale them primarily based on some particular person worth. However what worth ought to we use? Probably the most cheap alternative is to make use of their preliminary worth at time 0, earlier than they had been influenced by no matter therapy we’re making use of to them.

So we additionally want to make use of one other vector, named val_t_0 that represents the worth of the person at time 0.

# value_kaplan_meier: array containing the Worth Kaplan-Meier estimates
# obs_t: array, whether or not a topic has been noticed at time t
# val_t_0: array, consumer worth at time 0
# val_t: array, consumer worth at time t
# val_t_minus_1: array, consumer worth at time t−1

value_rate_t = (
    (val_t[obs_t] / val_t_0[obs_t]).sum()
    / (val_t_minus_1[obs_t] / val_t_0[obs_t]).sum()
)

value_kaplan_meier[t] = value_kaplan_meier[t-1] * value_rate_t

What we’ve constructed is a direct generalization of Kaplan-Meier. Actually, for those who set val_t = surv_t, val_t_minus_1 = surv_t_minus_1, and val_t_0 as an array of 1s, this components collapses neatly again to our authentic survival estimator. So sure—it’s legit.

And right here is the curve that we’d get hold of when utilized to those 3 customers.

Let’s name this new model the Worth Kaplan-Meier estimator. Actually, it solutions the query:

How a lot % of worth remains to be surviving, on common, after x time?

We’ve bought the speculation. However does it work within the wild?

Utilizing Worth Kaplan-Meier in observe

In the event you take the Worth Kaplan-Meier estimator for a spin on real-world information and evaluate it to the great previous Kaplan-Meier curve, you’ll seemingly discover one thing comforting — they usually have the identical form. That’s a superb signal. It means we haven’t damaged something elementary whereas upgrading from binary to steady.

However right here’s the place issues get fascinating: Worth Kaplan-Meier often sits a bit above its conventional cousin. Why? As a result of on this new world, customers are allowed to “resurrect”. Kaplan-Meier, being the extra inflexible of the 2, would’ve written them off the second they went quiet.

So how can we put this to make use of?

Think about you’re operating an experiment. At time zero, you begin a brand new therapy on a bunch of customers. No matter it’s, you possibly can observe how a lot worth “survives” in each the therapy and management teams over time.

And that is what your output will in all probability appear to be:

Conclusion

Kaplan-Meier is a broadly used and intuitive technique for estimating survival capabilities, particularly when the result is a binary occasion like dying or failure. Nevertheless, many real-world enterprise situations contain extra complexity — resurrections are attainable, and outcomes are higher represented by steady values slightly than a binary state.

In such instances, Worth Kaplan-Meier presents a pure extension. By incorporating the financial worth of people over time, it permits a extra nuanced understanding of worth retention and decay. This technique preserves the simplicity and interpretability of the unique Kaplan-Meier estimator whereas adapting it to higher mirror the dynamics of buyer conduct.

Worth Kaplan-Meier tends to supply the next estimate of retained worth in comparison with Kaplan-Meier, on account of its capability to account for recoveries. This makes it significantly helpful in evaluating experiments or monitoring buyer worth over time.