Generate constant assignments on the fly throughout completely different implementation environments
A core a part of operating an experiment is to assign an experimental unit (as an example a buyer) to a selected remedy (fee button variant, advertising push notification framing). Usually this project wants to fulfill the next circumstances:
- It must be random.
- It must be steady. If the shopper comes again to the display, they should be uncovered to the identical widget variant.
- It must be retrieved or generated in a short time.
- It must be out there after the precise project so it may be analyzed.
When organizations first begin their experimentation journey, a typical sample is to pre-generate assignments, retailer it in a database after which retrieve it on the time of project. It is a completely legitimate methodology to make use of and works nice while you’re beginning off. Nevertheless, as you begin to scale in buyer and experiment volumes, this methodology turns into more durable and more durable to keep up and use reliably. You’ve acquired to handle the complexity of storage, be certain that assignments are literally random and retrieve the project reliably.
Utilizing ‘hash areas’ helps clear up a few of these issues at scale. It’s a very easy resolution however isn’t as extensively often known as it in all probability ought to. This weblog is an try at explaining the method. There are hyperlinks to code in several languages on the finish. Nevertheless for those who’d like you too can straight bounce to code right here.
We’re operating an experiment to check which variant of a progress bar on our buyer app drives probably the most engagement. There are three variants: Management (the default expertise), Variant A and Variant B.
We have now 10 million prospects that use our app each week and we wish to be certain that these 10 million prospects get randomly assigned to one of many three variants. Every time the shopper comes again to the app they need to see the identical variant. We wish management to be assigned with a 50% chance, Variant 1 to be assigned with a 30% chance and Variant 2 to be assigned with a 20% chance.
probability_assignments = {"Management": 50, "Variant 1": 30, "Variant 2": 20}
To make issues less complicated, we’ll begin with 4 prospects. These prospects have IDs that we use to consult with them. These IDs are usually both GUIDs (one thing like "b7be65e3-c616-4a56-b90a-e546728a6640") or integers (like 1019222, 1028333). Any of those ID sorts would work however to make issues simpler to comply with we’ll merely assume that these IDs are: “Customer1”, “Customer2”, “Customer3”, “Customer4”.
This methodology primarily depends on utilizing hash algorithms that include some very fascinating properties. Hashing algorithms take a string of arbitrary size and map it to a ‘hash’ of a set size. The simplest option to perceive that is by some examples.
A hash operate, takes a string and maps it to a continuing hash area. Within the instance beneath, a hash operate (on this case md5) takes the phrases: “Hi there”, “World”, “Hi there World” and “Hi there WorLd” (word the capital L) and maps it to an alphanumeric string of 32 characters.
A couple of necessary issues to notice:
- The hashes are all the similar size.
- A minor distinction within the enter (capital L as a substitute of small L) adjustments the hash.
- Hashes are a hexadecimal string. That’s, they comprise of the numbers 0 to 9 and the primary six alphabets (a, b, c, d, e and f).
We are able to use this similar logic and get hashes for our 4 prospects:
import hashlibrepresentative_customers = ["Customer1", "Customer2", "Customer3", "Customer4"]
def get_hash(customer_id):
hash_object = hashlib.md5(customer_id.encode())
return hash_object.hexdigest()
{buyer: get_hash(buyer) for buyer in representative_customers}
# {'Customer1': 'becfb907888c8d48f8328dba7edf6969',
# 'Customer2': '0b0216b290922f789dd3efd0926d898e',
# 'Customer3': '2c988de9d49d47c78f9f1588a1f99934',
# 'Customer4': 'b7ca9bb43a9387d6f16cd7b93a7e5fb0'}
Hexadecimal strings are simply representations of numbers in base 16. We are able to convert them to integers in base 10.
⚠️ One necessary word right here: We not often want to make use of the complete hash. In follow (as an example within the linked code) we use a a lot smaller a part of the hash (first 10 characters). Right here we use the complete hash to make explanations a bit simpler.
def get_integer_representation_of_hash(customer_id):
hash_value = get_hash(customer_id)
return int(hash_value, 16){
buyer: get_integer_representation_of_hash(buyer)
for buyer in representative_customers
}
# {'Customer1': 253631877491484416479881095850175195497,
# 'Customer2': 14632352907717920893144463783570016654,
# 'Customer3': 59278139282750535321500601860939684148,
# 'Customer4': 244300725246749942648452631253508579248}
There are two necessary properties of those integers:
- These integers are steady: Given a set enter (“Customer1”), the hashing algorithm will all the time give the identical output.
- These integers are uniformly distributed: This one hasn’t been defined but and principally applies to cryptographic hash capabilities (comparable to md5). Uniformity is a design requirement for these hash capabilities. In the event that they weren’t uniformly distributed, the probabilities of collisions (getting the identical output for various inputs) could be larger and weaken the safety of the hash. There are some explorations of the uniformity property.
Now that we’ve got an integer illustration of every ID that’s steady (all the time has the identical worth) and uniformly distributed, we are able to use it to get to an project.
Going again to our chance assignments, we wish to assign prospects to variants with the next distribution:
{"Management": 50, "Variant 1": 30, "Variant 2": 20}
If we had 100 slots, we are able to divide them into 3 buckets the place the variety of slots represents the chance we wish to assign to that bucket. As an illustration, in our instance, we divide the integer vary 0–99 (100 models), into 0–49 (50 models), 50–79 (30 models) and 80–99 (20 models).
def divide_space_into_partitions(prob_distribution):
partition_ranges = []
begin = 0
for partition in prob_distribution:
partition_ranges.append((begin, begin + partition))
begin += partition
return partition_rangesdivide_space_into_partitions(prob_distribution=probability_assignments.values())
# word that that is zero listed, decrease sure inclusive and higher sure unique
# [(0, 50), (50, 80), (80, 100)]
Now, if we assign a buyer to one of many 100 slots randomly, the resultant distribution ought to then be equal to our supposed distribution. One other approach to consider that is, if we select a quantity randomly between 0 and 99, there’s a 50% probability it’ll be between 0 and 49, 30% probability it’ll be between 50 and 79 and 20% probability it’ll be between 80 and 99.
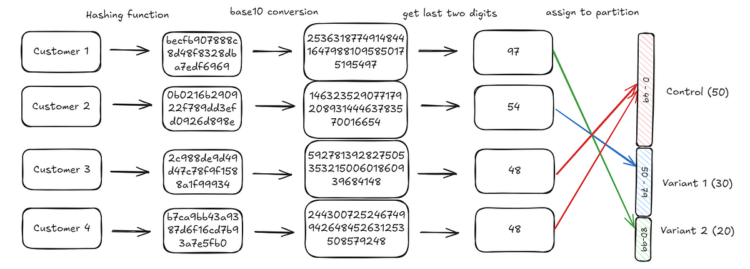
The one remaining step is to map the shopper integers we generated to one in every of these hundred slots. We do that by extracting the final two digits of the integer generated and utilizing that because the project. As an illustration, the final two digits for buyer 1 are 97 (you possibly can verify the diagram beneath). This falls within the third bucket (Variant 2) and therefore the shopper is assigned to Variant 2.
We repeat this course of iteratively for every buyer. Once we’re achieved with all our prospects, we should always discover that the top distribution might be what we’d count on: 50% of shoppers are in management, 30% in variant 1, 20% in variant 2.
def assign_groups(customer_id, partitions):
hash_value = get_relevant_place_value(customer_id, 100)
for idx, (begin, finish) in enumerate(partitions):
if begin <= hash_value < finish:
return idx
return Nonepartitions = divide_space_into_partitions(
prob_distribution=probability_assignments.values()
)
teams = {
buyer: listing(probability_assignments.keys())[assign_groups(customer, partitions)]
for buyer in representative_customers
}
# output
# {'Customer1': 'Variant 2',
# 'Customer2': 'Variant 1',
# 'Customer3': 'Management',
# 'Customer4': 'Management'}
The linked gist has a replication of the above for 1,000,000 prospects the place we are able to observe that prospects are distributed within the anticipated proportions.
# ensuing proportions from a simulation on 1 million prospects.
{'Variant 1': 0.299799, 'Variant 2': 0.199512, 'Management': 0.500689