Present code
library(tibble)
library(ggplot2)
library(dplyr)
library(tidyr)
library(latex2exp)
library(scales)
library(knitr)Over the previous few years working in advertising measurement, I’ve seen that energy evaluation is among the most poorly understood testing and measurement subjects. Generally it’s misunderstood and typically it’s not utilized in anyway regardless of its foundational position in take a look at design. This text and the sequence that comply with are my makes an attempt to alleviate this.
On this phase, I’ll cowl:
- What’s statistical energy?
- How can we compute it?
- What can affect energy?
Energy evaluation is a statistical subject and as a consequence, there might be math and statistics (loopy proper?) however I’ll attempt to tie these technical particulars again to actual world issues or primary instinct each time potential.
With out additional ado, let’s get to it.
Error varieties in testing: Kind I vs. Kind II
In testing, there are two kinds of error:
- Kind I:
- Technical Definition: We erroneously reject the null speculation when the null speculation is true
- Layman’s Definition: We are saying there was an impact when there actually wasn’t
- Instance: A/B testing a brand new inventive and concluding that it performs higher than the previous design when in actuality, each designs carry out the identical
- Kind II:
- Technical Definition: We fail to reject the null speculation when the null speculation is fake
- Layman’s Definition: We are saying there was no impact when there actually was
- Instance: A/B testing a brand new inventive and concluding that it performs the identical because the previous design when in actuality, the brand new design performs higher
What’s statistical energy?
Most individuals are aware of Kind I error. It’s the error that we management by setting a significance stage. Energy pertains to Kind II error. Extra particularly, energy is the chance of accurately rejecting the null speculation when it’s false. It’s the complement of Kind II error (i.e., 1 – Kind II error). In different phrases, energy is the chance of detecting a real impact if one exists. It must be clear why that is essential:
- Underpowered checks are prone to miss true results, resulting in missed alternatives for enchancment
- Underpowered checks can result in false confidence within the outcomes, as we could conclude that there is no such thing as a impact when there really is one
- … and most easily, underpowered checks waste cash and sources
The position of α and β
If each are essential, why are Kind II error and energy so misunderstood and ignored whereas Kind I is at all times thought of? It’s as a result of we are able to simply decide our Kind I error price. In reality, that’s precisely what we’re doing after we set the importance stage α (sometimes α = 0.05) for our checks. We’re stating that we’re snug with a sure proportion of Kind I error. Throughout take a look at setup, we make an announcement, “we’re snug with an X % false constructive price,” after which set α = X %. After the take a look at, if our p-value falls under α, we reject the null speculation (i.e., “the outcomes are important”), and if the p-value falls above α, we fail to reject the null speculation (i.e., “the outcomes should not important”).
Figuring out Kind II error, β (sometimes β = 0.20), and thus energy, will not be as easy. It requires us to make assumptions and carry out evaluation, referred to as “energy evaluation.” To grasp the method, it’s greatest to first stroll by the method of testing after which backtrack to determine how energy will be computed and influenced. Let’s use a easy A/B inventive take a look at for example.
| Idea | Image | Typical Worth(s) | Technical Definition | Plain-Language Definition |
|---|---|---|---|---|
| Kind I Error | α | 0.05 (5%) | Likelihood of rejecting the null speculation when the null is definitely true | Saying there’s an impact when in actuality there is no such thing as a distinction |
| Kind II Error | β | 0.20 (20%) | Likelihood of failing to reject the null speculation when the null is definitely false | Saying there is no such thing as a impact when in actuality there’s one |
| Energy | 1 − β | 0.80 (80%) | Likelihood of accurately rejecting the null speculation when the choice is true | The possibility we detect a real impact if there’s one |
Computing energy: step-by-step
A pair notes earlier than we get began:
- I made a couple of assumptions and approximations to simplify the instance. If you happen to can spot them, nice. If not, don’t fear about it. The purpose is to know the ideas and course of, not the nitty gritty particulars.
- I confer with the choice threshold within the z-score area because the essential worth. Crucial worth sometimes refers back to the threshold within the unique area (e.g., conversion charges) however I’ll use it interchangeably so I don’t have to introduce a brand new time period.
- There are code snippets all through tied to the textual content and ideas. If you happen to copy the code your self, you may mess around with the parameters to see how issues change. A few of the code snippets are hidden to maintain the article readable. Click on “Present the code” to see the code.
- Do that: Edit the pattern measurement within the take a look at setup in order that the take a look at statistic is just under the essential worth after which run the ability evaluation. Are the outcomes what you anticipated?
Check setup and the take a look at statistic
As said above, it’s greatest to stroll by the testing course of first after which backtrack to establish how energy will be computed. Let’s do exactly that.
# Set parameters for the A/B take a look at
N_a <- 1000 # Pattern measurement for inventive A
N_b <- 1000 # Pattern measurement for inventive B
alpha <- 0.05 # Significance stage
# Perform to compute the essential z-value for a one-tailed take a look at
critical_z <- operate(alpha, two_sided = FALSE) {
if (two_sided) qnorm(1 - alpha/2) else qnorm(1 - alpha)
}As said above, it’s greatest to stroll by the testing course of first after which backtrack to establish how energy will be computed. Let’s do exactly that.
Our take a look at setup:
- Null speculation: The conversion price of A equals the conversion price of B.
- Various speculation: The conversion price of B is bigger than the conversion price of A.
- Pattern measurement:
- Na = 1,000 — Quantity of people that obtain inventive A
- Nb = 1,000 — Quantity of people that obtain inventive B
- Significance stage: α = 0.05
- Crucial worth: The essential worth is the z-score that corresponds to the importance stage α. We name this Z1−α. For a one-tailed take a look at with α = 0.05, that is roughly 1.64.
- Check kind: Two-proportion z-test
x_a <- 100 # Variety of conversions for inventive A
x_b <- 150 # Variety of conversions for inventive B
p_a <- x_a / N_a # Conversion price for inventive A
p_b <- x_b / N_b # Conversion price for inventive BOur outcomes:
- xa = 100 — Variety of conversions from inventive A
- xb = 150 — Variety of conversions from inventive B
- pa = xa / Na = 0.10 — Conversion price of inventive A
- pb = xb / Nb = 0.15 — Conversion price of inventive B
Underneath the null speculation, the distinction in conversion charges follows an roughly regular distribution with:
- Imply: μ = 0 (no distinction in conversion charges)
- Normal deviation:
σ = √[ pa(1 − pa)/Na + pb(1 − pb)/Nb ] ≈ 0.01
z_score <- operate(p_a, p_b, N_a, N_b) {
(p_b - p_a) / sqrt((p_a * (1 - p_a) / N_a) + (p_b * (1 - p_b) / N_b))
}From these values, we are able to compute the take a look at statistic:
[
z = frac{p_b – p_a}
{sqrt{frac{p_a (1 – p_a)}{N_a} + frac{p_b (1 – p_b)}{N_b}}}
approx 3.39
]
If our take a look at statistic, z, is bigger than the essential worth, we reject the null speculation and conclude that Artistic B performs higher than Artistic A. If z is lower than or equal to the essential worth, we fail to reject the null speculation and conclude that there is no such thing as a important distinction between the 2 creatives.
In different phrases, if our outcomes are unlikely to be noticed when the conversion charges of A and B are actually the identical, we reject the null speculation and state that Artistic B performs higher than Artistic A. In any other case, we fail to reject the null speculation and state that there is no such thing as a important distinction between the 2 creatives.
Given our take a look at outcomes, we reject the null speculation and conclude that Artistic B performs higher than Artistic A.
z <- z_score(p_a, p_b, N_a, N_b)
critical_value <- critical_z(alpha)
if (z > critical_value) {
outcome <- "Reject null speculation: Artistic B performs higher than Artistic A"
} else {
outcome <- "Fail to reject null speculation: No important distinction between creatives"
}
outcome
#> [1] "Reject null speculation: Artistic B performs higher than Artistic A"The instinct behind energy
Now that we’ve walked by the testing course of, the place does energy come into play? Within the course of above, we report pattern conversion charges, pa and pb, after which compute the take a look at statistic, z. Nevertheless, if we repeated the take a look at many instances, we might get totally different pattern conversion charges and totally different take a look at statistics, all centering across the true conversion charges of the creatives.
Assume the true conversion price of Artistic B is greater than that of Artistic A. A few of these checks will nonetheless fail to reject the null speculation as a consequence of pure variance. Energy is the share of those checks that reject the null speculation. That is the underlying mechanism behind all energy evaluation and hints on the lacking ingredient: the true conversion charges—or extra typically, the true impact measurement.
Intuitively, if the true impact measurement is greater, our measured impact would sometimes be greater and we’d reject the null speculation extra typically, growing energy.
Selecting the true impact measurement
If we’d like true conversion charges to compute energy, how can we get them? If we had them, we wouldn’t have to carry out testing. Due to this fact, we have to make an assumption. Broadly, there are two approaches:
- Select the significant impact measurement: On this method, we assign the true impact measurement (or true distinction in conversion charges) to a stage that will be significant. If Artistic B solely elevated conversion charges by 0.01%, would we really care and take motion on these outcomes? Most likely not. So why would we care about having the ability to detect that small of an impact? However, if Artistic B elevated conversion charges by 50%, we actually would care. In observe, the significant impact measurement seemingly falls between these two factors.
- Observe: That is sometimes called the minimal detectable impact. Nevertheless, the minimal detectable impact of the research and the minimal detectable impact that we care about (for instance, we could solely care about 5% or better results, however the research is designed to detect 1% or better results) could differ. For that purpose, I favor to make use of the time period significant impact when referring to this technique.
- Use prior research: If we’ve information from prior research or fashions that measure the effectivity of this inventive or related creatives, we are able to use these values to assign the true impact measurement.
Each of the above approaches are legitimate.
If you happen to solely care to see significant results and don’t thoughts if you happen to miss out on detecting smaller results, go together with the primary choice. If you happen to should see “statistical significance”, go together with the second choice and be conservative with the values you employ (extra on that in one other article).
Technical Observe
As a result of we don’t have true conversion charges, we’re technically assigning a selected anticipated distribution to the choice speculation after which computing energy based mostly on that. The true imply within the following passages is technically the anticipated imply beneath the choice speculation. I’ll use the time period true to maintain the language easy and concise.
Computing and visualizing energy
Now that we’ve the lacking substances, true conversion charges, we are able to compute energy. As a substitute of the measured pa and pb, we now have true conversion charges ra and rb.
We measure energy as:
[
1 – beta = 1 – P(z < Z_{1-alpha} ;|; N_a, N_b, r_a, r_b)
]
This can be complicated at first look, so let’s break it down.
We’re stating that energy (1 − β) is computed by subtracting the Kind II error price from one. The Kind II error price is the chance {that a} take a look at leads to a z-score under our significance threshold, given our pattern measurement and true conversion charges ra and rb. How can we compute that final half?
In a two-proportion z-score take a look at, we all know that:
- Imply: μ = rb − ra
- Normal deviation: σ = √[ ra(1 − ra)/Na + rb(1 − rb)/Nb ]
Now we have to compute:
[
P(X > Z_{1-alpha}), quad X sim N!left(frac{mu}{sigma},,1right)
]
That is the world beneath the above distribution that lies to the precise of Z1−α and is equal to computing:
[
P!left(X > frac{mu}{sigma} – Z_{1-alpha}right), quad X sim N(0,1)
]
If we had a textbook with a z-score desk, we may merely search for the p-value related to
(μ / σ − Z1−α), and that will give us the ability.
Let’s present this visually:
Present the code
r_a <- p_a # true baseline conversion price; we're reusing the measured worth
r_b <- p_b # true remedy conversion price; we're reusing the measure worth
alpha <- 0.05
two_sided <- FALSE # set TRUE for two-sided take a look at
mu_diff <- operate(r_a, r_b) r_b - r_a
sigma_diff <- operate(r_a, r_b, N_a, N_b) {
sqrt(r_a*(1 - r_a)/N_a + r_b*(1 - r_b)/N_b)
}
power_value <- operate(r_a, r_b, N_a, N_b, alpha, two_sided = FALSE) {
mu <- mu_diff(r_a, r_b)
sd1 <- sigma_diff(r_a, r_b, N_a, N_b)
zc <- critical_z(alpha, two_sided)
thr <- zc * sigma_diff(r_a, r_b, N_a, N_b)
if (!two_sided) {
1 - pnorm(thr, imply = mu, sd = sd1)
} else {
pnorm(-thr, imply = mu, sd = sd1) + (1 - pnorm(thr, imply = mu, sd = sd1))
}
}
# Construct plot information
mu <- mu_diff(r_a, r_b)
sd1 <- sigma_diff(r_a, r_b, N_a, N_b)
zc <- critical_z(alpha, two_sided)
thr <- zc * sigma_diff(r_a, r_b, N_a, N_b)
# x-range overlaying each curves and thresholds
x_min <- min(-4*sd1, mu - 4*sd1, -thr) - 0.1*sd1
x_max <- max( 4*sd1, mu + 4*sd1, thr) + 0.1*sd1
xx <- seq(x_min, x_max, size.out = 2000)
df <- tibble(
x = xx,
H0 = dnorm(xx, imply = 0, sd = sd1), # distribution utilized by take a look at threshold
H1 = dnorm(xx, imply = mu, sd = sd1) # true (various) distribution
)
# Areas to shade for energy
if (!two_sided) {
shade <- df %>% filter(x >= thr)
} else {
shade <- bind_rows(
df %>% filter(x >= thr),
df %>% filter(x <= -thr)
)
}
# Numeric energy for subtitle
pow <- power_value(r_a, r_b, N_a, N_b, alpha, two_sided)
# Plot
ggplot(df, aes(x = x)) +
# H1 shaded energy area
geom_area(
information = shade, aes(y = H1), alpha = 0.25
) +
# Curves
geom_line(aes(y = H0), linewidth = 1) +
geom_line(aes(y = H1), linewidth = 1, linetype = "dashed") +
# Crucial line(s)
geom_vline(xintercept = thr, linetype = "dotted", linewidth = 0.8) +
{ if (two_sided) geom_vline(xintercept = -thr, linetype = "dotted", linewidth = 0.8) } +
# Imply markers
geom_vline(xintercept = 0, alpha = 0.3) +
geom_vline(xintercept = mu, alpha = 0.3, linetype = "dashed") +
# Labels
labs(
title = "Energy as shaded space beneath H1 past essential threshold",
subtitle = TeX(sprintf(r"($1 - beta$ = %.1f%% | $mu$ = %.4f, $sigma$ = %.4f, $z^*$ = %.3f, threshold = %.4f)",
100*pow, mu, sd1, zc, thr)),
x = TeX(r"(Distinction in conversion charges ($D = p_b - p_a$))"),
y = "Density"
) +
annotate("textual content", x = mu, y = max(df$H1)*0.95, label = TeX(r"(H1: $N(mu, sigma^2)$)"), hjust = -0.05) +
annotate("textual content", x = 0, y = max(df$H0)*0.95, label = TeX(r"(H0: $N(0, sigma^2)$)"), hjust = 1.05) +
theme_minimal(base_size = 13)
Within the plot above, energy is the world beneath the choice distribution (H1) (the place we assume the choice is distributed in line with our true conversion charges) that’s past the essential threshold (i.e., the world the place we reject the null speculation). With the parameters we set, the ability is 0.96. Because of this if we repeated this take a look at many instances with the identical parameters, we might anticipate to reject the null speculation roughly 96% of the time.
Energy curves
Now that we’ve instinct and math behind energy, we are able to discover how energy adjustments based mostly on totally different parameters. The plots generated from such evaluation are referred to as energy curves.
Observe
All through the plots, you’ll discover that 80% energy is highlighted. It is a widespread goal for energy in testing, because it balances the danger of Kind II error with the price of growing pattern measurement or adjusting different parameters. You’ll see this worth highlighted in lots of software program packages as a consequence.
Relationship with impact measurement
Earlier, I said that the bigger the impact measurement, the upper the ability. Intuitively, this is smart. We’re primarily shifting the precise bell curve within the plot above additional to the precise, so the world past the essential threshold will increase. Let’s take a look at that principle.
Present the code
# Perform to compute energy for various impact sizes
power_curve <- operate(effect_sizes, N_a, N_b, alpha, two_sided = FALSE) {
sapply(effect_sizes, operate(e) {
r_a <- p_a
r_b <- p_a + e # Modify r_b based mostly on impact measurement
power_value(r_a, r_b, N_a, N_b, alpha, two_sided)
})
}
# Generate impact sizes
effect_sizes <- seq(0, 0.1, size.out = 100) # Impact sizes from 0 to 10%
# Compute energy for every impact measurement
power_values <- power_curve(effect_sizes, N_a, N_b, alpha)
# Create a knowledge body for plotting
power_df <- tibble(
effect_size = effect_sizes,
energy = power_values
)
# Plot the ability curve
ggplot(power_df, aes(x = effect_size, y = energy)) +
geom_line(coloration = "blue", measurement = 1) +
geom_hline(yintercept = 0.80, linetype = "dashed", alpha = 0.6) + # goal energy information
labs(
title = "Energy vs. Impact Dimension",
x = TeX(r"(Impact Dimension ($r_b - r_a$))"),
y = TeX(r'(Energy ($1 - beta $))')
) +
scale_x_continuous(labels = scales::percent_format(accuracy = 0.01)) +
scale_y_continuous(labels = scales::percent_format(accuracy = 1), limits = c(NA,1)) +
theme_minimal(base_size = 13)
Concept confirmed: because the impact measurement will increase, energy will increase. It approaches 100% because the impact measurement will increase and our resolution threshold strikes down the long-tail of the traditional distribution.
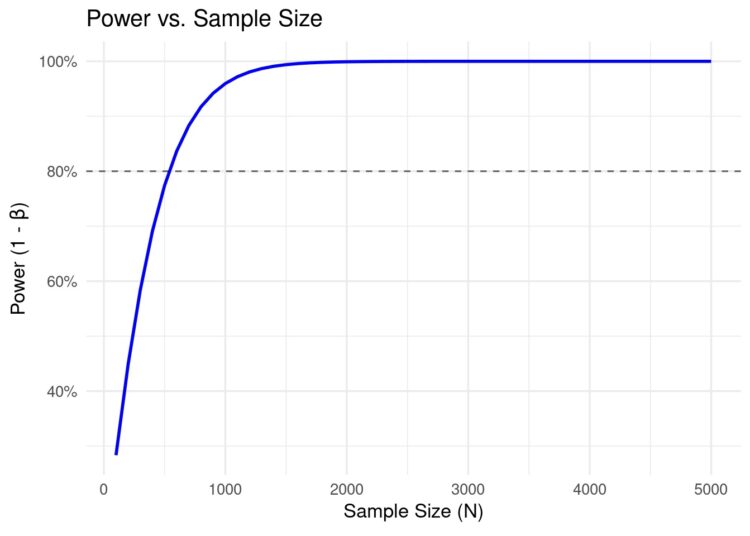
Relationship with pattern measurement
Sadly, we can’t management impact measurement. It’s both the significant impact measurement you want to detect or based mostly on prior research. It’s what it’s. What we are able to management is pattern measurement. The bigger the pattern measurement, the smaller the usual deviation of the distribution and the bigger the world beneath the curve past the essential threshold (think about squeezing the edges to compress the bell curves within the plot earlier). In different phrases, bigger pattern sizes ought to result in greater energy. Let’s take a look at this principle as effectively.
Present the code
power_sample_size <- operate(N_a, N_b, r_a, r_b, alpha, two_sided = FALSE) {
power_value(r_a, r_b, N_a, N_b, alpha, two_sided)
}
# Generate pattern sizes
sample_sizes <- seq(100, 5000, by = 100) # Pattern sizes from 100 to 5000
# Compute energy for every pattern measurement
power_values_sample <- sapply(sample_sizes, operate(N) {
power_sample_size(N, N, r_a, r_b, alpha)
})
# Create a knowledge body for plotting
power_sample_df <- tibble(
sample_size = sample_sizes,
energy = power_values_sample
)
# Plot the ability curve for various pattern sizes
ggplot(power_sample_df, aes(x = sample_size, y = energy)) +
geom_line(coloration = "blue", measurement = 1) +
geom_hline(yintercept = 0.80, linetype = "dashed", alpha = 0.6) + # goal energy information
labs(
title = "Energy vs. Pattern Dimension",
x = TeX(r"(Pattern Dimension ($N$))"),
y = TeX(r"(Energy (1 - $beta$))")
) +
scale_y_continuous(labels = scales::percent_format(accuracy = 1), limits = c(NA,1)) +
theme_minimal(base_size = 13)
We once more see the anticipated relationship: as pattern measurement will increase, energy will increase.
Observe
On this particular setup, we are able to enhance energy by growing pattern measurement. Extra typically, this is a rise in precision. In different take a look at setups, precision—and thus energy—will be elevated by different means. For instance, in Geo-testing, we are able to enhance precision by choosing predictable markets or by the inclusion of exogenous options (extra on this in a future article).
Relationship with significance stage
Does the importance stage α affect energy? Intuitively, if we’re extra prepared to just accept Kind I error, we usually tend to reject the null speculation and thus (1 − β) must be greater. Let’s take a look at this principle.
Present the code
power_of_alpha <- operate(alpha_vec, r_a, r_b, N_a, N_b, two_sided = FALSE) {
sapply(alpha_vec, operate(a)
power_value(r_a, r_b, N_a, N_b, a, two_sided)
)
}
alpha_grid <- seq(0.001, 0.20, size.out = 400)
power_grid <- power_of_alpha(alpha_grid, r_a, r_b, N_a, N_b, two_sided)
# Present level
power_now <- power_value(r_a, r_b, N_a, N_b, alpha, two_sided)
df_alpha_power <- tibble(alpha = alpha_grid, energy = power_grid)
ggplot(df_alpha_power, aes(x = alpha, y = energy)) +
geom_line(coloration = "blue", measurement = 1) +
geom_hline(yintercept = 0.80, linetype = "dashed", alpha = 0.6) + # goal energy information
geom_vline(xintercept = alpha, linetype = "dashed", alpha = 0.6) + # your alpha
scale_x_continuous(labels = scales::percent_format(accuracy = 1)) +
scale_y_continuous(labels = scales::percent_format(accuracy = 1), limits = c(NA,1)) +
labs(
title = TeX(r"(Energy vs. Significance Degree)"),
subtitle = TeX(sprintf(r"(At $alpha$ = %.1f%%, $1 - beta$ = %.1f%%)",
100*alpha, 100*power_now)),
x = TeX(r"(Significance Degree ($alpha$))"),
y = TeX(r"(Energy (1 - $beta$))")
) +
theme_minimal(base_size = 13)
But once more, the outcomes match our instinct. There is no such thing as a free lunch in statistics. All else equal, if we wish to lower our Kind II error price (β), we have to be prepared to just accept a better Kind I price (α).
Energy evaluation
So what’s energy evaluation? Energy evaluation is the method of computing energy given the parameters of the take a look at. In energy evaluation, we repair parameters we can’t management after which optimize the parameters we are able to management to attain a desired energy stage. For instance, we are able to repair the true impact measurement after which compute the pattern measurement wanted to attain a desired energy stage. Energy curves are sometimes used to help with this decision-making course of. Later within the sequence, I’ll stroll by energy evaluation intimately with a real-world instance.
Sources
[1] R. Larsen and M. Marx, An Introduction to Mathematical Statistics and Its Functions
What’s subsequent within the Sequence?
I haven’t absolutely determined however I positively wish to cowl the next subjects:
- Energy evaluation in Geo Testing
- Detailed information on setting the true impact measurement in varied contexts
- Actual world end-to-end examples
Completely satisfied to listen to concepts. Be happy to achieve out. My contact information is under: