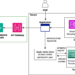
Figuring out and Gathering key Information
I explored a number of algorithms to optimize and cut back the search area for all attainable combos. Nevertheless, the truth that every card can seem twice elevated the variety of potential combos, making it difficult to trace and validate each. Whereas competing on Codeforces, I encountered an issue that jogged my memory of the ‘island downside,’ which gave me new perception into approaching the hand evaluator system.
We are able to symbolize the hand as a 2D grid of measurement 4×13, the place every column represents ranks from 1 to 13 and every row corresponds to the 4 fits. Every cell on this grid accommodates the depend of playing cards within the hand in our case both 1, 2, or 0 . This enables us to divide the hand into ‘islands,’ that are outlined as teams of linked land cells with counts of 1 or 2 based mostly on the next connectivity guidelines:
1. Two cells are thought-about linked in the event that they share a facet (left, proper, above, or under) within the grid.
2. All cells throughout the similar column are additionally linked in the event that they each include at the very least 1s, even when they aren’t adjoining (above or under).
EXP of ‘ hand A’ : 11C 3H 4H 11D 3D 5H 9D 2H 6H 3C 4H 3D 4D 5H 12D 3C
Our first activity is to establish and label all distinct islands. Since every island is unbiased of the others, we will make our life simpler by mapping every island to a category sort let’s identify it _cardGraph. This class shall be accountable for that island when it comes to extracting, modifying, or deleting operations.
For readability, let’s isolate one island and work on it within the upcoming sections, so it’s simpler so that you can comply with. If it helps, you’ll be able to consider every island as a linked graph, as Proven within the determine under:
Now Should you take a number of island examples and attempt to extract the attainable combos, you’ll discover that some playing cards have distinctive roles in branching out to a possible mixtures. We’ll name these sort of playing cards a management factors or Cpts for brief, as they play a necessary position by decreasing the search area considerably as you will note within the following steps.
Cpts: For a card to be thought-about a Cpts, it should be able the place we’ve got to choose on which meld (run or set) to append it to. If a card can naturally match into a number of melds with out forcing a selection (for instance, a replica card with two choices for melds every card will append to a meld), it received’t be thought-about a Cpts.
Within the case of our island instance the three of coronary heart is recognized as a cpts. Under are all of the melds that the three of Hearts might connect to, one after the other.
Our subsequent step is to mark every card that qualifies as a Cpts. To do that, we’ll create a 4×13 (in byte sort) desk lets name it _flagMap . Now for reminiscence effectivity, you may make this a shared desk every _cardGraph occasion created from the hand can reference it and use it . On this desk, every card in an island shall be assigned a bitstream on the corresponding index in _flagMap, this byte will represents its potential placements in several runs or units. If a card qualifies as a Cpts, will probably be saved in a stack (we’ll want later), which we’ll name _cptsStack. Right here’s a breakdown of the byte construction: the primary bit signifies whether or not the cardboard belongs to a run, the second bit signifies its placement in an extra run, the third bit represents whether or not it belongs to a set, and the fourth bit specifies if it belongs to a number of units.
Right here’s an instance of a bitstream: 00000111 In right here we’ve got:
• The primary bit (1) means the cardboard can belong to a run.
• The second bit (1) means the cardboard can belong to a second run.
• The third bit (1) means the cardboard belongs to a set.
• The fourth bit (0) means the cardboard doesn’t belong to a second set.
We is perhaps in case the place the configuration is 00000101 for one card (no copy), that means the cardboard belongs to a run or a set. Or one other configuration might be 00000011, that means the cardboard belongs to 2 completely different runs.
To establish a cpts, merely depend the ‘1’s in its bit illustration. If this depend exceeds the entire variety of that card within the hand, it’s thought-about a cpts. For example, if a card seems twice (i.e., has two copies) and its bit illustration is 00000101, it’s not a cpts. Nevertheless, if the bit illustration is 00000111 like the instance , then it qualifies as a cpts.
In our island instance, right here’s how the _flagMap desk would look :
As soon as we’ve populated the _flagMap and recognized the cpts, the subsequent activity is to decompose the island into horizontal and vertical strains. However why? Breaking down the cardboard graph into these strains simplifies the method of figuring out runs and units, because it permits us to concentrate on contiguous sequences of playing cards that may be processed extra effectively. As you may guess, the vertical strains will symbolize the units, whereas the horizontal strains will symbolize the runs.
We’ll retailer every horizontal line in an inventory of a tuple sort, the place the primary merchandise represents the beginning index of the road and the final merchandise represents the top index (inclusive). For the vertical strains, it’s enough to easily retailer the column index in an inventory.
Tip: We are able to accomplish this activity together with the bit illustration step in a single loop, attaining O(n) complexity.
Generate Combos
Now, let’s take a break and recap: we’ve got recognized the management factors (CPTs) and saved them within the _cptsStack. We additionally decomposed the island into vertical and horizontal strains, and populated the _flagMap with card bit illustration.
With our knowledge in place, what stays is to make use of it to generate all attainable legitimate combos of the island. However how can we try this? Right here’s a simplified strategy:
1. Assign Legitimate Placements for the Management Factors (Cpts):
We take the bit illustration of a cpts from _flagMap, which signifies all attainable placements for that cpts. Then, we take a look at the variety of copies of the cpts within the _cardGraph and alter its bit illustration to a present legitimate configuration. For instance, if the cpts has a bit illustration of 00001111 and a pair of copies, we will generate all legitimate placements for it, which is C(4,2)=6C(4,2) = 6C(4,2)=6. Attainable mixtures could be 0011, 0101, 1100, 1010, 1001, and 0110.
2. Utilizing DFS to Configure All Attainable Mixtures for Every Cpts:
We’ll use a depth-first search (DFS) to iterate over the legitimate placements for every cpts as proven in step 1. Every node within the DFS tree represents a attainable placement for a given cpts, so every distinctive DFS path represents a legitimate combo configuration. For every “leaf” node (finish of the DFS path), we proceed to the subsequent step.
3. Producing Combos:
On this step, we iterate over the horizontal and vertical strains within the island to establish runs, units, and a dump record. That is executed in two passes for every line, as follows:
- Cross 1: For a horizontal line, for instance, we constantly append playing cards from [line start to line end] into an inventory to kind a run. We cease including if ( card_bit_representation | 00000001 == 0 ). If the size of the run is larger than or equal to three, we add it to the run combo; in any other case, every card goes into the dump record, and we proceed attempting to kind one other run till we attain the road finish.
- Cross 2: Repeat the method, this time in search of playing cards that match a special bit sample with or operation ( 00000010). This enables us to establish attainable second runs.
The identical strategy applies to extracting units, however we use bit operations with 00000100 and 00001000.
4. Register the Legitimate Combo and Transfer to the Subsequent DFS Configuration:
After finishing all runs, units, and dumps for the present combo, we save the combo after which transfer on to the subsequent DFS configuration to repeat the method. This manner, we systematically discover all potential configurations for legitimate combos.
in case you coded every thing appropriately and feed it our island instance : ”2H3H4H5H4H5H6H3C3C3D3D4D”, it ought to be decomposed as proven bellow. Discover that I’ve added some calculation to every generated combo in order that we will get a way of how the AI will act.
Within the subsequent article, I’ll dive into the remainder of the system, specializing in the dynamic modification of the hand and the AI technique. Should you’ve adopted alongside to date, it received’t be exhausting to see how we will optimize including and eradicating playing cards, in addition to incorporate the 2 guidelines we put aside in the beginning. Keep tuned, and see you subsequent time! “hopefully 😉”.
Until in any other case famous, all pictures are created by the creator utilizing Lucidchart ,Gimp and Python