Introduction
My earlier posts regarded on the bog-standard choice tree and the marvel of a random forest. Now, to finish the triplet, I’ll visually discover !
There are a bunch of gradient boosted tree libraries, together with XGBoost, CatBoost, and LightGBM. Nonetheless, for this I’m going to make use of sklearn’s one. Why? Just because, in contrast with the others, it allowed me to visualise simpler. In observe I have a tendency to make use of the opposite libraries greater than the sklearn one; nevertheless, this undertaking is about visible studying, not pure efficiency.
Essentially, a GBT is a mix of bushes that solely work collectively. Whereas a single choice tree (together with one extracted from a random forest) could make an honest prediction by itself, taking a person tree from a GBT is unlikely to provide something usable.
Past this, as all the time, no concept, no maths — simply plots and hyperparameters. As earlier than, I’ll be utilizing the California housing dataset by way of scikit-learn (CC-BY), the identical common course of as described in my earlier posts, the code is at https://github.com/jamesdeluk/data-projects/tree/principal/visualising-trees, and all photographs beneath are created by me (aside from the GIF, which is from Tenor).
A primary gradient boosted tree
Beginning with a primary GBT: gb = GradientBoostingRegressor(random_state=42). Just like different tree sorts, the default settings for min_samples_split, min_samples_leaf, max_leaf_nodes are 2, 1, None respectively. Apparently, the default max_depth is 3, not None as it’s with choice bushes/random forests. Notable hyperparameters, which I’ll look into extra later, embrace learning_rate (how steep the gradient is, default 0.1), and n_estimators (just like random forest — the variety of bushes).
Becoming took 2.2s, predicting took 0.005s, and the outcomes:
| Metric | max_depth=None |
|---|---|
| MAE | 0.369 |
| MAPE | 0.216 |
| MSE | 0.289 |
| RMSE | 0.538 |
| R² | 0.779 |
So, faster than the default random forest, however barely worse efficiency. For my chosen block, it predicted 0.803 (precise 0.894).
Visualising
Because of this you’re right here, proper?
The tree
Just like earlier than, we will plot a single tree. That is the primary one, accessed with gb.estimators_[0, 0]:

I’ve defined these within the earlier posts, so I received’t achieve this once more right here. One factor I’ll carry to your consideration although: discover how horrible the values are! Three of the leaves even have destructive values, which we all know can’t be the case. Because of this a GBT solely works as a mixed ensemble, not as separate standalone bushes like in a random forest.
Predictions and errors
My favorite technique to visualise GBTs is with prediction vs iteration plots, utilizing gb.staged_predict. For my chosen block:

Bear in mind the default mannequin has 100 estimators? Nicely, right here they’re. The preliminary prediction was approach off — 2! However every time it learnt (keep in mind learning_rate?), and obtained nearer to the actual worth. After all, it was educated on the coaching information, not this particular information, so the ultimate worth was off (0.803, so about 10% off), however you’ll be able to clearly see the method.
On this case, it reached a reasonably regular state after about 50 iterations. Later we’ll see the best way to cease iterating at this stage, to keep away from losing money and time.
Equally, the error (i.e. the prediction minus the true worth) might be plotted. After all, this offers us the identical plot, merely with totally different y-axis values:

Let’s take this one step additional! The check information has over 5000 blocks to foretell; we will loop by way of every, and predict all of them, for every iteration!

I like this plot.

All of them begin round 2, however explode throughout the iterations. We all know all of the true values range from 0.15 to five, with a imply of two.1 (test my first publish), so this spreading out of predictions (from ~0.3 to ~5.5) is as anticipated.
We are able to additionally plot the errors:

At first look, it appears a bit unusual — we’d count on them to begin at, say, ±2, and converge on 0. Trying rigorously although, this does occur for many — it may be seen within the left-hand aspect of the plot, the primary 10 iterations or so. The issue is, with over 5000 traces on this plot, there are a number of overlapping ones, making the outliers stand out extra. Maybe there’s a greater technique to visualise these? How about…

The median error is 0.05 — which is excellent! The IQR is lower than 0.5, which can also be respectable. So, whereas there are some horrible predictions, most are respectable.
Hyperparameter tuning
Choice tree hyperparameters
Identical as earlier than, let’s examine how the hyperparameters explored within the authentic choice tree publish apply to GBTs, with the default hyperparameters of learning_rate = 0.1, n_estimators = 100. The min_samples_leaf, min_samples_split, and max_leaf_nodes one even have max_depth = 10, to make it a good comparability to earlier posts and to one another.
| Mannequin | max_depth=None | max_depth=10 | min_samples_leaf=10 | min_samples_split=10 | max_leaf_nodes=100 |
|---|---|---|---|---|---|
| Match Time (s) | 10.889 | 7.009 | 7.101 | 7.015 | 6.167 |
| Predict Time (s) | 0.089 | 0.019 | 0.015 | 0.018 | 0.013 |
| MAE | 0.454 | 0.304 | 0.301 | 0.302 | 0.301 |
| MAPE | 0.253 | 0.177 | 0.174 | 0.174 | 0.175 |
| MSE | 0.496 | 0.222 | 0.212 | 0.217 | 0.210 |
| RMSE | 0.704 | 0.471 | 0.46 | 0.466 | 0.458 |
| R² | 0.621 | 0.830 | 0.838 | 0.834 | 0.840 |
| Chosen Prediction | 0.885 | 0.906 | 0.962 | 0.918 | 0.923 |
| Chosen Error | 0.009 | 0.012 | 0.068 | 0.024 | 0.029 |
In contrast to choice bushes and random forests, the deeper tree carried out far worse! And took longer to suit. Nonetheless, growing the depth from 3 (the default) to 10 has improved the scores. The opposite constraints resulted in additional enhancements — once more exhibiting how all hyperparameters can play a task.
learning_rate
GBTs function by tweaking predictions after every iteration based mostly on the error. The upper the adjustment (a.okay.a. the gradient, a.okay.a. the educational charge), the extra the prediction modifications between iterations.
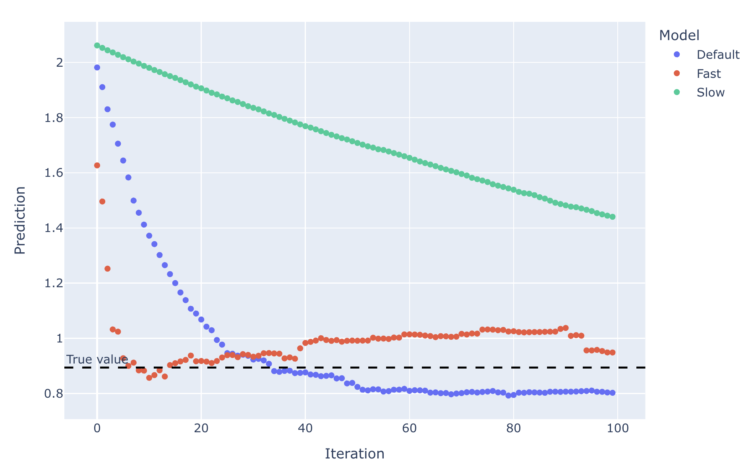
There’s a clear trade-off for studying charge. Evaluating studying charges of 0.01 (Sluggish), 0.1 (Default), and 0.5 (Quick), over 100 iterations:

Sooner studying charges can get to the right worth faster, however they’re extra prone to overcorrect and bounce previous the true worth (assume fishtailing in a automobile), and may result in oscillations. Sluggish studying charges could by no means attain the right worth (assume… not turning the steering wheel sufficient and driving straight right into a tree). As for the stats:
| Mannequin | Default | Quick | Sluggish |
|---|---|---|---|
| Match Time (s) | 2.159 | 2.288 | 2.166 |
| Predict Time (s) | 0.005 | 0.004 | 0.015 |
| MAE | 0.370 | 0.338 | 0.629 |
| MAPE | 0.216 | 0.197 | 0.427 |
| MSE | 0.289 | 0.247 | 0.661 |
| RMSE | 0.538 | 0.497 | 0.813 |
| R² | 0.779 | 0.811 | 0.495 |
| Chosen Prediction | 0.803 | 0.949 | 1.44 |
| Chosen Error | 0.091 | 0.055 | 0.546 |
Unsurprisingly, the sluggish studying mannequin was horrible. For this block, quick was barely higher than the default total. Nonetheless, we will see on the plot how, not less than for the chosen block, it was the final 90 iterations that obtained the quick mannequin to be extra correct than the default one — if we’d stopped at 40 iterations, for the chosen block not less than, the default mannequin would have been much better. The fun of visualisation!
n_estimators
As talked about above, the variety of estimators goes hand in hand with the educational charge. Basically, the extra estimators the higher, because it offers extra iterations to measure and alter for the error — though this comes at an extra time price.
As seen above, a sufficiently excessive variety of estimators is very vital for a low studying charge, to make sure the right worth is reached. Growing the variety of estimators to 500:

With sufficient iterations, the sluggish studying GBT did attain the true worth. Actually, all of them ended up a lot nearer. The stats verify this:
| Mannequin | DefaultMore | FastMore | SlowMore |
|---|---|---|---|
| Match Time (s) | 12.254 | 12.489 | 11.918 |
| Predict Time (s) | 0.018 | 0.014 | 0.022 |
| MAE | 0.323 | 0.319 | 0.410 |
| MAPE | 0.187 | 0.185 | 0.248 |
| MSE | 0.232 | 0.228 | 0.338 |
| RMSE | 0.482 | 0.477 | 0.581 |
| R² | 0.823 | 0.826 | 0.742 |
| Chosen Prediction | 0.841 | 0.921 | 0.858 |
| Chosen Error | 0.053 | 0.027 | 0.036 |
Unsurprisingly, growing the variety of estimators five-fold elevated the time to suit considerably (on this case by six-fold, however that will simply be a one-off). Nonetheless, we nonetheless haven’t surpassed the scores of the constrained bushes above — I assume we’ll must do a hyperparameter search to see if we will beat them. Additionally, for the chosen block, as might be seen within the plot, after about 300 iterations not one of the fashions actually improved. If that is constant throughout all the information, then the additional 700 iterations have been pointless. I discussed earlier about the way it’s doable to keep away from losing time iterating with out enhancing; now’s time to look into that.
n_iter_no_change, validation_fraction, and tol
It’s doable for extra iterations to not enhance the ultimate consequence, but it nonetheless takes time to run them. That is the place early stopping is available in.
There are three related hyperparameters. The primary, n_iter_no_change, is what number of iterations for there to be “no change” earlier than doing no extra iterations. tol[erance] is how huge the change in validation rating must be to be labeled as “no change”. And validation_fraction is how a lot of the coaching information for use as a validation set to generate the validation rating (word that is separate from the check information).
Evaluating a 1000-estimator GBT with one with a reasonably aggressive early stopping — n_iter_no_change=5, validation_fraction=0.1, tol=0.005 — the latter one stopped after solely 61 estimators (and therefore solely took 5~6% of the time to suit):

As anticipated although, the outcomes have been worse:
| Mannequin | Default | Early Stopping |
|---|---|---|
| Match Time (s) | 24.843 | 1.304 |
| Predict Time (s) | 0.042 | 0.003 |
| MAE | 0.313 | 0.396 |
| MAPE | 0.181 | 0.236 |
| MSE | 0.222 | 0.321 |
| RMSE | 0.471 | 0.566 |
| R² | 0.830 | 0.755 |
| Chosen Prediction | 0.837 | 0.805 |
| Chosen Error | 0.057 | 0.089 |
However as all the time, the query to ask: is it price investing 20x the time to enhance the R² by 10%, or decreasing the error by 20%?
Bayes looking
You have been most likely anticipating this. The search areas:
search_spaces = {
'learning_rate': (0.01, 0.5),
'max_depth': (1, 100),
'max_features': (0.1, 1.0, 'uniform'),
'max_leaf_nodes': (2, 20000),
'min_samples_leaf': (1, 100),
'min_samples_split': (2, 100),
'n_estimators': (50, 1000),
}Most are just like my earlier posts; the one further hyperparameter is learning_rate.
It took the longest up to now, at 96 minutes (~50% greater than the random forest!) The very best hyperparameters are:
best_parameters = OrderedDict({
'learning_rate': 0.04345459461297153,
'max_depth': 13,
'max_features': 0.4993693929975871,
'max_leaf_nodes': 20000,
'min_samples_leaf': 1,
'min_samples_split': 83,
'n_estimators': 325,
})max_features, max_leaf_nodes, and min_samples_leaf, are similar to the tuned random forest. n_estimators is just too, and it aligns with what the chosen block plot above prompt — the additional 700 iterations have been largely pointless. Nonetheless, in contrast with the tuned random forest, the bushes are solely a 3rd as deep, and min_samples_split is much greater than we’ve seen up to now. The worth of learning_rate was not too stunning based mostly on what we noticed above.
And the cross-validated scores:
| Metric | Imply | Std |
|---|---|---|
| MAE | -0.289 | 0.005 |
| MAPE | -0.161 | 0.004 |
| MSE | -0.200 | 0.008 |
| RMSE | -0.448 | 0.009 |
| R² | 0.849 | 0.006 |
Of all of the fashions up to now, that is the most effective, with smaller errors, greater R², and decrease variances!
Lastly, our previous good friend, the field plots:

Conclusion
And so we come to the tip of my mini-series on the three most typical varieties of tree-based fashions.
My hope is that, by seeing other ways of visualising bushes, you now (a) higher perceive how the totally different fashions operate, with out having to have a look at equations, and (b) can use your personal plots to tune your personal fashions. It might additionally assist with stakeholder administration — execs favor fairly photos to tables of numbers, so exhibiting them a tree plot may help them perceive why what they’re asking you to do is inconceivable.
Based mostly on this dataset, and these fashions, the gradient boosted one was barely superior to the random forest, and each have been far superior to a lone choice tree. Nonetheless, this will have been as a result of the GBT had 50% extra time to seek for higher hyperparameters (they sometimes are extra computationally costly — in any case, it was the identical variety of iterations). It’s additionally price noting that GBTs have the next tendency to overfit than random forests. And whereas the choice tree had worse efficiency, it’s far sooner — and in some use instances, that is extra vital. Moreover, as talked about, there are different libraries, with execs and cons — for instance, CatBoost handles categorical information out of the field, whereas different GBT libraries sometimes require categorical information to be preprocessed (e.g. one-hot or label encoding). Or, in case you’re feeling actually courageous, how about stacking the totally different tree sorts in an ensemble for even higher efficiency…
Anyway, till subsequent time!