One of many predominant issues that arises in high-dimensional density estimation is that as our dimension will increase, our information turns into extra sparse. Due to this fact, for fashions that depend on native neighborhood estimation we’d like exponentially extra information as our dimension will increase to proceed getting significant outcomes. That is known as the curse of dimensionality.
In my earlier article on density estimation, I demonstrated how the kernel density estimator (KDE) could be successfully used for one-dimensional information. Nonetheless, its efficiency deteriorates considerably in greater dimensions. As an instance this, I ran a simulation to find out what number of samples are required for KDE to attain a imply relative error of 0.2 when estimating the density of a multivariate Gaussian distribution throughout varied dimensions. Bandwidth was chosen utilizing Scott’s rule. The outcomes are as follows:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity
from sklearn.model_selection import GridSearchCV
np.random.seed(42)
# Gaussian pattern generator
def generate_gaussian_samples(n_samples, dim, imply=0, std=1):
return np.random.regular(imply, std, measurement=(n_samples, dim))
def compute_bandwidth(samples):
# Scott technique
n, d = samples.form
return np.energy(n, -1./(d + 4))
# KDE error computation
def compute_kde_error(samples, dim, n_test=1000):
bandwidth = compute_bandwidth(samples)
kde = KernelDensity(bandwidth=bandwidth).match(samples)
test_points = np.random.regular(0, 1, measurement=(n_test, dim))
kde_density = np.exp(kde.score_samples(test_points))
true_density = np.exp(-np.sum(test_points**2, axis=1) / 2) / ((2 * np.pi)**(dim / 2))
error = np.imply(np.abs(kde_density - true_density) / true_density)
return error, bandwidth
# Decide required samples for a goal error
def find_required_samples(dim, target_error=0.2, max_samples=500000, start_samples=10, n_experiments=5):
samples = start_samples
whereas samples <= max_samples:
errors = [compute_kde_error(generate_gaussian_samples(samples, dim), dim)[0] for _ in vary(n_experiments)]
avg_error = np.imply(errors)
if avg_error <= target_error:
return samples, avg_error
samples = int(samples * 1.5)
return max_samples, avg_error
# Principal
def analyze_kde(dims, target_error):
outcomes = []
for dim in dims:
samples, error = find_required_samples(dim, target_error)
outcomes.append((dim, samples))
print(f"Dim {dim}: {samples} samples")
return outcomes
# Visualization
def plot_results(dims, outcomes,target_error=.2):
samples = [x[1] for x in outcomes]
plt.determine(figsize=(8, 6))
plt.plot(dims, samples, 'o-', shade='blue')
plt.yscale('log')
plt.xlabel('Dimension')
plt.ylabel('Required Variety of Samples (log scale)')
plt.title(f'Samples Wanted for a Imply Relative Error of {target_error}')
plt.grid(True)
for i, pattern in enumerate(samples):
plt.textual content(dims[i], pattern * 1.15, f'{pattern}', fontsize=10, ha='proper', shade='black')
plt.present()
# Run the evaluation
dims = vary(1, 7)
target_error = 0.2
outcomes = analyze_kde(dims, target_error)
plot_results(dims, outcomes)
That’s proper: in my simulation, to match the accuracy of simply 22 information factors in a single dimension, you would wish greater than 360,000 information factors in six dimensions! Much more astonishingly, in his ebook Multivariate Density Estimation, David W. Scott reveals that, relying on the metric, over one million information factors are required in eight dimensions to attain the identical accuracy as simply 50 information factors in a single dimension.
Hopefully, this is sufficient to persuade you that the kernel density estimator just isn’t splendid for estimating densities in greater dimensions. However what’s the choice?
Half 2: Introduction to Normalizing Flows
One promising various is Normalizing Flows, and the particular mannequin I’ll deal with is the Masked Autoregressive Move (MAF).
This part attracts partly on the work of George Papamakarios and Balaji Lakshminarayanan, as introduced in Chapter 23 of Probabilistic Machine Studying: Superior Matters by Kevin P. Murphy (see the ebook for additional particulars).
The core concept behind normalizing flows is {that a} distribution p(x) could be modeled by beginning with random variables sampled from a easy base distribution, (resembling a Gaussian) after which passing them by way of a sequence of differentiable, invertible transformations (diffeomorphisms). Every transformation incrementally reshapes the distribution, regularly mapping the bottom distribution into the goal distribution. A visible illustration of this course of is proven beneath.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
np.random.seed(42)
#Pattern from a typical regular distribution
n_points = 1000
initial_dist = np.random.regular(loc=[0, 0], scale=1.0, measurement=(n_points, 2))
#Generate goal distribution
theta = np.linspace(0, np.pi, n_points//2)
r = 2
x1 = r * np.cos(theta)
y1 = r * np.sin(theta)
x2 = (r-0.5) * np.cos(theta)
y2 = (r-0.5) * np.sin(theta) - 1
target_dist = np.vstack([
np.column_stack([x1, y1 + 0.5]),
np.column_stack([x2, y2 + 0.5])
])
target_dist += np.random.regular(0, 0.1, target_dist.form)
def f1(x, t):
"""Cut up transformation"""
shift = 2 * t * np.signal(x[:, 1])[:, np.newaxis] * np.array([1, 0])
return x + shift
def f2(x, t):
"""Curve transformation"""
theta = t * np.pi / 2
r = np.sqrt(x[:, 0]**2 + x[:, 1]**2)
phi = np.arctan2(x[:, 1], x[:, 0]) + theta * (1 - r/4)
return np.column_stack([r * np.cos(phi), r * np.sin(phi)])
def f3(x, t):
"""Fantastic-tune to focus on"""
return (1 - t) * x + t * target_dist
# Create determine
fig, ax = plt.subplots(figsize=(10, 10))
scatter = ax.scatter([], [], alpha=0.6, s=10)
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
def sigmoid(x):
"""Clean transition perform"""
return 1 / (1 + np.exp(-(x - 0.5) * 10))
def get_title(t):
if t < 0.33:
return f'Making use of Cut up Transformation (f₁)'
elif t < 0.66:
return f'Making use of Curve Transformation (f₂)'
else:
return f'Fantastic-tuning to Goal Distribution (f₃)'
def init():
scatter.set_offsets(initial_dist)
ax.set_title('Preliminary Gaussian Distribution', pad=20, fontsize=18)
return [scatter]
def replace(body):
#Normalize body to [0, 1]
t = body / 100
#Apply transformations sequentially
factors = initial_dist
#f1: Cut up the distribution
t1 = sigmoid(t * 3) if t < 0.33 else 1
factors = f1(factors, t1)
#f2: Create curves
t2 = sigmoid((t - 0.33) * 3) if 0.33 <= t < 0.66 else (0 if t < 0.33 else 1)
factors = f2(factors, t2)
#f3: Fantastic-tune to focus on
t3 = sigmoid((t - 0.66) * 3) if t >= 0.66 else 0
factors = f3(factors, t3)
#Replace scatter plot
scatter.set_offsets(factors)
colours = factors[:, 0] + factors[:, 1]
scatter.set_array(colours)
#Replace title
ax.set_title(get_title(t), pad=20, fontsize=18)
return [scatter]
#Create animation
anim = FuncAnimation(fig, replace, frames=100, init_func=init,
interval=50, blit=True)
plt.tight_layout()
plt.present()
#Save animation as a gif
anim.save('normalizing_flow_single.gif', author='pillow')Extra formally, assume the next:

Then our goal distribution is outlined by the next change of variables system:

The place J_{f^{-1}}(x), the Jacobian of f^{-1} evaluated at x.
Since we have to compute the determinant, there’s additionally a computational consideration; our transformation features ought to ideally have Jacobians whose determinants are simple to calculate. Designing a diffeomorphic perform that each fashions a fancy distribution and yields a tractable determinant is a difficult activity. The way in which that is addressed in observe is by setting up the goal distribution by way of a movement of easier features. Thus, f is outlined as follows:

Then, because the composition of diffeomorphic features can be diffeomorphic, f can be invertible and differentiable.
There are a number of typical candidates for f. Listed beneath are well-liked decisions.
Affine Flows
Affine flows are given by the next perform:

We have to prohibit A to being an invertible sq. matrix in order that f is invertible. Affine flows should not superb at modelling information on their very own, however they’re helpful when blended with different features.
Elementwise Flows
Elementwise flows remodel the vector u factor smart. Let h be a scalar bijection, we are able to create a vector-valued bijection f outlined as follows:

The determinant of the Jacobian is then given by:

Just like affine flows, elementwise flows should not very efficient at modeling information on their very own, since they don’t seize interactions between dimensions. Nonetheless, they’re usually utilized in mixture with different transformations to construct extra advanced flows.
Coupling Flows
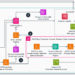
Coupling flows, launched by Dinh et al. (2015), differ from the flows mentioned earlier in that they permit using non-linear features to higher seize the construction of the information. Apologies for utilizing a picture right here, however to keep away from confusion I wanted inline LaTeX.

Right here, the parameters of f-hat are calculated by sending the subset b of u by way of Θ, the place Θ is a common perform known as the conditioner. This setup contrasts with affine flows, which solely combine dimensions linearly, and elementwise flows, which preserve every dimension remoted. Coupling flows permit for a non-linear mixing of dimensions by way of the conditioner. If you’re eager about the kind of coupling layers which were proposed, see Kobyzev, Ivan & Prince, Simon & Brubaker, Marcus. (2020).
The determinant is sort of easy to calculate because the partial spinoff of x-b with respect to u-b is 0. Therefore, the Jacobian is the next higher block triangular matrix:

The determinant of the Jacobian is then given by:

The next showcases visually how every of those features might impact the distribution.

Masked Autoregressive Flows
Assume that u is a vector containing d components. An autoregressive bijection perform, which outputs a vector x with d components, is outlined as follows:

Right here, h is a scalar bijection parameterized by Θ, the place Θ is an arbitrary non-linear perform, usually a neural community. On account of the autoregressive construction, every factor x_i relies upon solely on the weather of u as much as the i-th index. Consequently, the Jacobian matrix can be triangular, and its determinant would be the product of the diagonal entries, as follows:


If we had been to make use of a number of autoregressive bijection features as our f, we would wish to coach d completely different neural networks, which could be fairly computationally costly. So as an alternative, to deal with this, a extra environment friendly method in observe is to share parameters between the conditioners by combining them right into a single mannequin Θ that takes in a shared enter x and outputs the set of parameters (Θ1, Θ2,…, Θd). Nonetheless, to maintain the autoregressive construction, we have now to make sure that every Θi relies upon solely on x1,x2,…,xi−1.
Masked Autoregressive Flows (MAF) use a multi-layer perceptron because the non-linear perform, after which apply masking to zero out any computational paths that might violate the autoregressive construction. By doing so, MAF ensures that every output Θi is conditionally dependent solely on the earlier inputs x1,x2,…,xi−1 and permitting for environment friendly coaching.
Half 3: Showdown
To find out whether or not KDE or MAF higher fashions distributions in greater dimensions, I designed an experiment that’s just like my introductory evaluation of KDE. I skilled each fashions on progressively bigger datasets till every achieved a KL divergence of 0.5.
For these unfamiliar with this metric, KL divergence quantifies how one likelihood distribution differs from a reference distribution. Particularly, it measures the anticipated extra ‘shock’ from utilizing one distribution to approximate one other. A KL divergence of 0.0 signifies excellent alignment between distributions, whereas greater values signify larger discrepancy. To offer visible instinct, the determine beneath illustrates what .5 KL divergence seems to be like when evaluating two three-dimensional distributions:

The experimental design encompassed three distinct distribution households, every chosen to check completely different points of the fashions’ capabilities. First, I examined Conditional Gaussian Distributions, which symbolize the best case with unimodal, symmetric likelihood mass. Second, I examined Conditional Combination of Gaussians, introducing multimodality to problem the fashions’ means to seize a number of distinct modes within the information. Lastly, I included Conditional Skew Regular distributions to evaluate efficiency on uneven distributions.
For the Kernel Density Estimation mannequin, choosing acceptable bandwidth parameters was difficult for the bigger dimensions. I ended up using Go away-One-Out Cross-Validation (LOOCV), a method the place every information level is held out whereas the remaining factors are used to estimate the optimum bandwidth. This course of, whereas computationally costly, requiring n separate mannequin matches for n information factors, was mandatory for reaching dependable ends in greater dimensions. In my earlier variations of this experiments with various bandwidth choice strategies, all demonstrated inferior efficiency, requiring considerably extra coaching information to attain the identical KL divergence threshold.
The Masked Autoregressive Move mannequin required a unique optimization technique. Like most neural community primarily based fashions, MAF is dependent upon a variety of hyperparameters. I developed a scaling technique the place these hyperparameters had been adjusted proportionally to the enter dimensionality. It’s necessary to notice that this scaling was primarily based on affordable heuristics reasonably than an exhaustive optimization. The hyperparameter search was stored minimal to determine baseline efficiency, extra subtle tuning would seemingly give massive efficiency enhancements for the MAF mannequin.
The whole codebase, together with information technology, mannequin implementations, coaching procedures, and analysis metrics, is offered in this repository for reproducibility and additional experimentation. Listed below are the outcomes:

The experimental outcomes present a hanging a distinction in relative efficiency of KDE and MAF! As proven by the graphs, a transition happens across the fifth dimension. Under this threshold, KDE confirmed higher efficiency, nonetheless, past 5 dimensions, MAF begins to vastly outperform KDE by more and more dramatic margins.
The magnitude of this distinction turns into stark at dimension 7, the place our outcomes reveal a profound disparity in information effectivity. Throughout all three distribution varieties examined KDE constantly required greater than 100,000 information factors to attain passable efficiency. In distinction, MAF reached the identical efficiency threshold with a most of merely a most of two,000 information factors throughout all distributions. This represents an enchancment issue starting from 50x to 100x!
Other than pattern effectivity, the computational efficiency variations are equally compelling because the KDE required roughly 12 occasions longer to coach than MAF at these greater dimensions.
The mixture of superior information effectivity and quicker coaching occasions makes MAF the clear winner for top dimensional duties. KDE remains to be actually a beneficial software for low-dimensional issues, however if you’re engaged on an software involving greater than 5 dimensions, I extremely advocate making an attempt the MAF method.
Half 4: Why does MAF Crush KDE?
To know this why KDE suffers in excessive dimension, we should first study how KDE really works underneath the hood. As mentioned in my earlier article, Kernel Density Estimation makes use of native neighborhood estimation, the place for any level the place we need to consider the density, KDE seems to be at close by information factors and makes use of their proximity to estimate the native likelihood density. Every kernel perform creates a neighborhood round every information level, and the density estimate at any location is the sum of contributions from all kernels whose neighborhoods embody that location.
This native method works effectively in low dimensions. Nonetheless, as the size improve, the information turns into sparser, inflicting the estimator to wish exponentially extra information factors to fill the area with the identical density.
In distinction, MAF doesn’t use native neighborhood primarily based estimation. As a substitute of estimating density by close by factors, MAF learns features that map earlier variables to conditional distribution parameters. The neural community’s weights are shared throughout your entire enter area, permitting it to generalize from coaching information without having to populate native neighborhoods. This architectural distinction permits MAF to scale much better then KDE with dimension.
This distinction between native and world approaches explains the dramatic efficiency hole noticed in my experiment. Whereas KDE should populate an exponentially increasing area with information factors to take care of correct native neighborhoods, MAF can exploit the compositional construction of neural networks to study world patterns utilizing far fewer samples.
Conclusion
The Kernel Density Estimator is nice at nonparametrically analyzing information in low dimensions; it’s intuitive, quick, and requires far much less tuning. Nonetheless, for top dimensional information, or when computational time is a priority, I’d advocate making an attempt out normalizing flows. Whereas the mannequin isn’t practically as battle examined as KDE, they’re a strong various to check out, and may simply find yourself being your new favourite density estimator.
Except in any other case famous, all photographs are by the creator. The code for the primary experiment is positioned on this repository.