On this article, I’ll introduce you to hierarchical Bayesian (HB) modelling, a versatile strategy to mechanically mix the outcomes of a number of sub-models. This methodology allows estimation of individual-level results by optimally combining data throughout completely different groupings of information via Bayesian updating. That is significantly helpful when particular person models have restricted observations however share frequent traits/behaviors with different models.
The next sections will introduce the idea, implementation, and various use circumstances for this methodology.
The Downside with Conventional Approaches
As an utility, think about that we’re a big grocery retailer making an attempt to maximise product-level income by setting costs. We would want to estimate the demand curve (elasticity) for every product, then optimize some revenue maximization perform. As step one to this workstream, we would want to estimate the value elasticity of demand (how responsive demand is to a 1% change in worth) given some longitudinal knowledge with $i in N$ merchandise over $t in T$ intervals. Do not forget that the value elasticity of demand is outlined as:
$$beta=frac{partial log{textrm{Items}}_{it}}{partial log textrm{Worth}_{it}}$$
Assuming no confounders, we will use a log-linear fixed-effect regression mannequin to estimate our parameter of curiosity:
$$log(textrm{Items}_{it})= beta log(textrm{Worth})_{it} +gamma_{c(i),t}+ delta_i+ epsilon_{it}$$
$gamma_{c(i),t}$ is a set of category-by-time dummy variables to seize the common demand in every category-time interval and $delta_i$ is a set of product dummies to seize the time-invariant demand shifter for every product. This “fixed-effect” formulation is commonplace and customary in lots of regression-based fashions to regulate for unobserved confounders. This (pooled) regression mannequin permits us to recuperate the common elasticity $beta$ throughout all $N$ models. This may imply that the shop might goal a median worth degree throughout all merchandise of their retailer to maximise the income:
$$underset{textrm{Worth}_t}{max} ;;; textrm{Worth}_{t}cdotmathbb{E}(textrm{Amount}_{t} | textrm{Worth}_{t}, beta)$$
If these models have a pure grouping (product classes), we’d have the ability to determine the common elasticity of every class by operating separate regressions (or interacting the value elasticity with the product class) for every class utilizing solely models from that class. This may imply that the shop might goal common costs in every class to maximise category-specific income, such that:
$$underset{textrm{Worth}_{c(i),t}}{max} ;;; textrm{Worth}_{c(i),t}cdotmathbb{E}(textrm{Amount}_{c(i),t} | textrm{Worth}_{c(i),t}, beta_{c(i)})$$
With adequate knowledge, we might even run separate regressions for every particular person product to acquire extra granular elasticities.
Nonetheless, real-world knowledge usually presents challenges: some merchandise have minimal worth variation, brief gross sales histories, or class imbalance throughout classes. Below these restrictions, operating separate regressions to determine product elasticity would probably result in giant commonplace errors and weak identification of $beta$. HB fashions addresses these points by permitting us to acquire granular estimates of the coefficient of curiosity by sharing statistical energy each throughout completely different groupings whereas preserving heterogeneity. With the HB formulation, it’s doable to run one single regression (just like the pooled case) whereas nonetheless recovering elasticities on the product degree, permitting for granular optimizations.
Understanding Hierarchical Bayesian Fashions
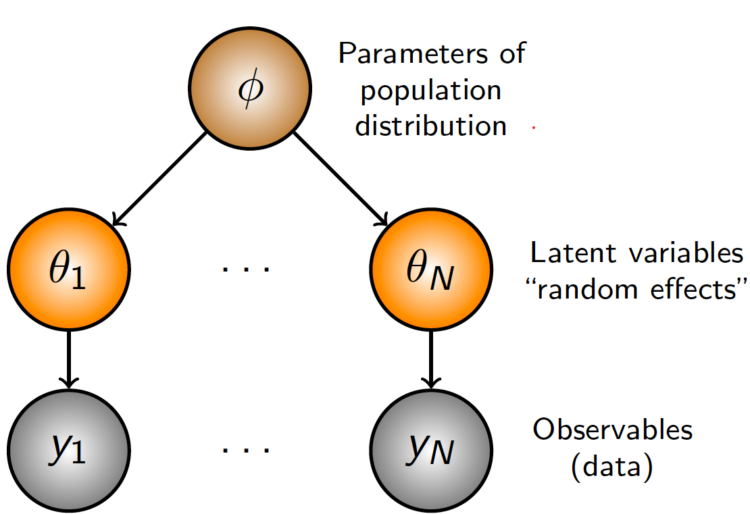
At its core, HB is about recognizing the pure construction in our knowledge. Quite than treating all observations as fully unbiased (many separate regressions) or forcing them to observe equivalent patterns (one pooled regression), we acknowledge that observations can cluster into teams, with merchandise inside every group sharing related patterns. The “hierarchical” side refers to how we arrange our parameters in numerous ranges. In its most simple format, we might have:
- A World parameter that applies to all knowledge.
- Group-level parameters that apply to observations inside that group.
- Particular person-level parameters that apply to every particular particular person.
This technique is versatile sufficient so as to add or take away hierarchies as wanted, relying on the specified degree of pooling. For instance, if we predict there are not any similarities throughout classes, we might take away the worldwide parameter. If we predict that these merchandise don’t have any pure groupings, we might take away the group-level parameters. If we solely care concerning the group-level impact, we will take away the individual-level parameter and have the group-level coefficients as our most granular parameter. If there exists the presence of subgroups nested inside the teams, we will add one other hierarchical layer. The chances are countless!
The “Bayesian” side refers to how we replace our beliefs about these parameters primarily based on noticed knowledge. We first begin with a proposed prior distribution that symbolize our preliminary perception of those parameters, then replace them iteratively to recuperate a posterior distributions that comes with the data from the info. In apply, because of this we use the global-level estimate to tell our group-level estimates, and the group-level parameters to tell the unit-level parameters. Items with a bigger variety of observations are allowed to deviate extra from the group-level means, whereas models with a restricted variety of observations are pulled nearer to the means.
Let’s formalize this with our worth elasticity instance, the place we (ideally) wish to recuperate the unit-level worth elasticity. We estimate:
$$log(textrm{Items}_{it})= beta_i log(textrm{Worth})_{it} +gamma_{c(i),t} + delta_i + epsilon_{it}$$
The place:
- $beta_i sim textrm{Regular}(beta_{cleft(iright)},sigma_i)$
- $beta_{c(i)}sim textrm{Regular}(beta_g,sigma_{c(i)})$
- $beta_gsim textrm{Regular}(mu,sigma)$
The one distinction from the primary equation is that we exchange the worldwide $beta$ time period with product-level betas $beta_i$. We specify that the unit degree elasticity $beta_i$ is drawn from a traditional distribution centered across the category-level elasticity common $beta_{c(i)}$, which is drawn from a shared international elasticity $beta_g$ for all teams. For the unfold of the distribution $sigma$, we will assume a hierarchical construction for that too, however on this instance, we simply set fundamental priors for them to keep up simplicity. For this utility, we assume a previous perception of: ${ mu= -2, sigma= 1, sigma_{c(i)}=1, sigma_i=1}$. This formulation of the prior assumes that the worldwide elasticity is elastic, 95% of the elasticities fall between -4 and 0, with a typical deviation of 1 at every hierarchical degree. To check whether or not these priors are accurately specified, we’d do a prior predictive checks (not lined on this article) to see whether or not our prior beliefs can recuperate the info that we observe.
This hierarchical construction permits data to circulation between merchandise in the identical class and throughout classes. If a specific product has restricted worth variation knowledge, its elasticity shall be pulled towards the class elasticity $beta_{c(i)}$. Equally, classes with fewer merchandise shall be influenced extra by the worldwide elasticity, which derives its imply from all class elasticities. The fantastic thing about this strategy is that the diploma of “pooling” occurs mechanically primarily based on the info. Merchandise with a number of worth variation will preserve estimates nearer to their particular person knowledge patterns, whereas these with sparse knowledge will borrow extra energy from their group.
Implementation
On this part, we implement the above mannequin utilizing the Numpyro package deal in Python, a light-weight probabilistic programming language powered by JAX for autograd and JIT compilation to GPU/TPU/CPU. We begin off by producing our artificial knowledge, defining the mannequin, and becoming the mannequin to the info. We shut out with some visualizations of the outcomes.
Knowledge Producing Course of
We simulate gross sales knowledge the place demand follows a log-linear relationship with worth and the product-level elasticity is generated from a Gaussian distribution $beta_i sim textrm{Regular}(-2, 0.7)$. We add in a random worth change each time interval with a $50%$ likelihood, category-specific time traits, and random noise. This provides in multiplicatively to generate our log anticipated demand. From the log anticipated demand, we exponentiate to get the precise demand, and draw realized models bought from a Poisson distribution. We then filter to maintain solely models with greater than 100 models bought (helps accuracy of estimates, not a obligatory step), and are left with $N=11,798$ merchandise over $T = 156$ intervals (weekly knowledge for 3 years). From this dataset, the true international elasticity is $beta_g = -1.6$, with category-level elasticities starting from $beta_{c(i)} in [-1.68, -1.48]$.
Understand that this DGP ignores plenty of real-world intricacies. We don’t mannequin any components that might collectively have an effect on each costs and demand (corresponding to promotions), and we don’t mannequin any confounders. This instance is only meant to point out that we will recuperate the product-specific elasticity beneath a wells-specified mannequin, and doesn’t goal to cowl tips on how to accurately determine that worth is exogenous. Nonetheless, I recommend that readers seek advice from Causal Inference for the Courageous and True for an introduction to causal inference.
import numpy as np
import pandas as pd
def generate_price_elasticity_data(N: int = 1000,
C: int = 10,
T: int = 50,
price_change_prob: float = 0.2,
seed = 42) -> pd.DataFrame:
"""
Generate artificial knowledge for worth elasticity of demand evaluation.
Knowledge is generated by
"""
if seed just isn't None:
np.random.seed(seed)
# Class demand and traits
category_base_demand = np.random.uniform(1000, 10000, C)
category_time_trends = np.random.uniform(0, 0.01, C)
category_volatility = np.random.uniform(0.01, 0.05, C) # Random volatility for every class
category_demand_paths = np.zeros((C, T))
category_demand_paths[:, 0] = 1.0
shocks = np.random.regular(0, 1, (C, T-1)) * category_volatility[:, np.newaxis]
traits = category_time_trends[:, np.newaxis] * np.ones((C, T-1))
cumulative_effects = np.cumsum(traits + shocks, axis=1)
category_demand_paths[:, 1:] = category_demand_paths[:, 0:1] + cumulative_effects
# product results
product_categories = np.random.randint(0, C, N)
product_a = np.random.regular(-2, .7, measurement=N)
product_a = np.clip(product_a, -5, -.1)
# Preliminary costs for every product
initial_prices = np.random.uniform(100, 1000, N)
costs = np.zeros((N, T))
costs[:, 0] = initial_prices
# Generate random values and whether or not costs modified
random_values = np.random.rand(N, T-1)
change_mask = random_values < price_change_prob
# Generate change components (-20% to +20%)
change_factors = 1 + np.random.uniform(-0.2, 0.2, measurement=(N, T-1))
# Create a matrix to carry multipliers
multipliers = np.ones((N, T-1))
# Apply change components solely the place modifications ought to happen
multipliers[change_mask] = change_factors[change_mask]
# Apply the modifications cumulatively to propagate costs
for t in vary(1, T):
costs[:, t] = costs[:, t-1] * multipliers[:, t-1]
# Generate product-specific multipliers
product_multipliers = np.random.lognormal(3, 0.5, measurement=N)
# Get time results for every product's class (form: N x T)
time_effects = category_demand_paths[product_categories][:, np.newaxis, :].squeeze(1)
# Guarantee time results do not go destructive
time_effects = np.most(0.1, time_effects)
# Generate interval noise for all merchandise and time intervals
period_noise = 1 + np.random.uniform(-0.05, 0.05, measurement=(N, T))
# Get class base demand for every product
category_base = category_base_demand[product_categories]
# Calculate base demand
base_demand = (category_base[:, np.newaxis] *
product_multipliers[:, np.newaxis] *
time_effects *
period_noise)
# log demand
alpha_ijt = np.log(base_demand)
# log worth
log_prices = np.log(costs)
# log anticipated demand
log_lambda = alpha_ijt + product_a[:, np.newaxis] * log_prices
# Convert again from log area to get fee parameters
lambda_vals = np.exp(log_lambda)
# Generate models bought
units_sold = np.random.poisson(lambda_vals) # Form: (N, T)
# Create index arrays for all combos of merchandise and time intervals
product_indices, time_indices = np.meshgrid(np.arange(N), np.arange(T), indexing='ij')
product_indices = product_indices.flatten()
time_indices = time_indices.flatten()
# Get classes for all merchandise
classes = product_categories[product_indices]
# Get all costs and models bought
all_prices = np.spherical(costs[product_indices, time_indices], 2)
all_units_sold = units_sold[product_indices, time_indices]
# Calculate elasticities
product_elasticity = product_a[product_indices]
df = pd.DataFrame({
'product': product_indices,
'class': classes,
'time_period': time_indices,
'worth': all_prices,
'units_sold': all_units_sold,
'product_elasticity': product_elasticity
})
return df
# Maintain solely models with >X gross sales
def filter_dataframe(df, min_units = 100):
temp = df[['product','units_sold']].groupby('product').sum().reset_index()
unit_filter = temp[temp.units_sold>min_units]['product'].distinctive()
filtered_df = df[df['product'].isin(unit_filter)].copy()
# Abstract
original_product_count = df['product'].nunique()
remaining_product_count = filtered_df['product'].nunique()
filtered_out = original_product_count - remaining_product_count
print(f"Filtering abstract:")
print(f"- Unique variety of merchandise: {original_product_count}")
print(f"- Merchandise with > {min_units} models: {remaining_product_count}")
print(f"- Merchandise filtered out: {filtered_out} ({filtered_out/original_product_count:.1%})")
# World and class elasticity
global_elasticity = filtered_df['product_elasticity'].imply()
filtered_df['global_elasticity'] = global_elasticity
# Class elasticity
category_elasticities = filtered_df.groupby('class')['product_elasticity'].imply().reset_index()
category_elasticities.columns = ['category', 'category_elasticity']
filtered_df = filtered_df.merge(category_elasticities, on='class', how='left')
# Abstract
print(f"nElasticity Info:")
print(f"- World elasticity: {global_elasticity:.3f}")
print(f"- Class elasticities vary: {category_elasticities['category_elasticity'].min():.3f} to {category_elasticities['category_elasticity'].max():.3f}")
return filtered_df
df = generate_price_elasticity_data(N = 20000, T = 156, price_change_prob=.5, seed=42)
df = filter_dataframe(df)
df.loc[:,'cat_by_time'] = df['category'].astype(str) + '-' + df['time_period'].astype(str)
df.head()
Filtering abstract:
- Unique variety of merchandise: 20000
- Merchandise with > 100 models: 11798
- Merchandise filtered out: 8202 (41.0%)
Elasticity Info:
- World elasticity: -1.598
- Class elasticities vary: -1.681 to -1.482
| product | class | time_period | worth | units_sold | product_elasticity | category_elasticity | global_elasticity | cat_by_time |
|---|---|---|---|---|---|---|---|---|
| 0 | 8 | 0 | 125.95 | 550 | -1.185907 | -1.63475 | -1.597683 | 8-0 |
| 0 | 8 | 1 | 125.95 | 504 | -1.185907 | -1.63475 | -1.597683 | 8-1 |
| 0 | 8 | 2 | 149.59 | 388 | -1.185907 | -1.63475 | -1.597683 | 8-2 |
| 0 | 8 | 3 | 149.59 | 349 | -1.185907 | -1.63475 | -1.597683 | 8-3 |
| 0 | 8 | 4 | 176.56 | 287 | -1.185907 | -1.63475 | -1.597683 | 8-4 |
Mannequin
We start by creating indices for merchandise, classes, and category-time combos utilizing pd.factorize(). This enables us to seelct the right parameter for every remark. We then convert the value (logged) and models collection into JAX arrays, then create plates that corresponds to every of our parameter teams. These plates retailer the parameters values for every degree of the hierarchy, together with storing the parameters representing the fastened results.
The mannequin makes use of NumPyro’s plate to outline the parameter teams:
global_a: 1 international worth elasticity parameter with a $textrm{Regular}(-2, 1)$ prior.category_a: $C=10$ category-level elasticities with priors centered on the worldwide parameter and commonplace deviation of 1.product_a: $N=11,798$ product-specific elasticities with priors centered on their respective class parameters and commonplace deviation of 1.product_effect: $N=11,798$ product-specific baseline demand results with a typical deviation of three.time_cat_effects: $(T=156)cdot(C=10)$ time-varying results particular to every category-time mixture with a typical deviation of three.
We then reparameterize the parameters utilizing The LocScaleReparam() argument to enhance sampling effectivity and keep away from funneling. After creating the parameters, we calculate log anticipated demand, then convert it again to a fee parameter with clipping for numerical stability. Lastly, we name on the info plate to pattern from a Poisson distribution with the calculated fee parameter. The optimization algorithm will then discover the values of the parameters that greatest match the info utilizing stochastic gradient descent. Beneath is a graphical illustration of the mannequin to point out the connection between the parameters.

import jax
import jax.numpy as jnp
import numpyro
import numpyro.distributions as dist
from numpyro.infer.reparam import LocScaleReparam
def mannequin(df: pd.DataFrame, final result: None):
# Outline indexes
product_idx, unique_product = pd.factorize(df['product'])
cat_idx, unique_category = pd.factorize(df['category'])
time_cat_idx, unique_time_cat = pd.factorize(df['cat_by_time'])
# Convert the value and models collection to jax arrays
log_price = jnp.log(df.worth.values)
final result = jnp.array(final result) if final result just isn't None else None
# Generate mapping
product_to_category = jnp.array(pd.DataFrame({'product': product_idx, 'class': cat_idx}).drop_duplicates().class.values, dtype=np.int16)
# Create the plates to retailer parameters
category_plate = numpyro.plate("class", unique_category.form[0])
time_cat_plate = numpyro.plate("time_cat", unique_time_cat.form[0])
product_plate = numpyro.plate("product", unique_product.form[0])
data_plate = numpyro.plate("knowledge", measurement=final result.form[0])
# DEFINING MODEL PARAMETERS
global_a = numpyro.pattern("global_a", dist.Regular(-2, 1), infer={"reparam": LocScaleReparam()})
with category_plate:
category_a = numpyro.pattern("category_a", dist.Regular(global_a, 1), infer={"reparam": LocScaleReparam()})
with product_plate:
product_a = numpyro.pattern("product_a", dist.Regular(category_a[product_to_category], 2), infer={"reparam": LocScaleReparam()})
product_effect = numpyro.pattern("product_effect", dist.Regular(0, 3))
with time_cat_plate:
time_cat_effects = numpyro.pattern("time_cat_effects", dist.Regular(0, 3))
# Calculating anticipated demand
def calculate_demand():
log_demand = product_a[product_idx]*log_price + time_cat_effects[time_cat_idx] + product_effect[product_idx]
expected_demand = jnp.exp(jnp.clip(log_demand, -4, 20)) # clip for stability
return expected_demand
demand = calculate_demand()
with data_plate:
numpyro.pattern(
"obs",
dist.Poisson(demand),
obs=final result
)
numpyro.render_model(
mannequin=mannequin,
model_kwargs={"df": df,"final result": df['units_sold']},
render_distributions=True,
render_params=True,
)
Estimation
Whereas there are a number of methods to estimate this equation, we use Stochastic Variational Inference (SVI) for this specific utility. As an outline, SVI is a gradient-based optimization methodology to reduce the KL-divergence between a proposed posterior distribution to the true posterior distribution by minimizing the ELBO. This can be a completely different estimation approach from Markov-Chain Monte Carlo (MCMC), which samples immediately from the true posterior distribution. In real-world functions, SVI is extra environment friendly and simply scales to giant datasets. For this utility, we set a random seed, initialize the information (household of posterior distribution, assumed to be a Diagonal Regular), outline the educational fee schedule and optimizer in Optax, and run the optimization for 1,000,000 (takes ~1 hour) iterations. Whereas the mannequin might need converged beforehand, the loss nonetheless improves by a minor quantity even after operating the optimization for 1,000,000 iterations. Lastly, we plot the (log) losses.

from numpyro.infer import SVI, Trace_ELBO, autoguide, init_to_sample
import optax
import matplotlib.pyplot as plt
rng_key = jax.random.PRNGKey(42)
information = autoguide.AutoNormal(mannequin, init_loc_fn=init_to_sample)
# Outline a studying fee schedule
learning_rate_schedule = optax.exponential_decay(
init_value=0.01,
transition_steps=1000,
decay_rate=0.99,
staircase = False,
end_value = 1e-5,
)
# Outline the optimizer
optimizer = optax.adamw(learning_rate=learning_rate_schedule)
svi = SVI(mannequin, information, optimizer, loss=Trace_ELBO(num_particles=8, vectorize_particles = True))
# Run SVI
svi_result = svi.run(rng_key, 1_000_000, df, df['units_sold'])
plt.semilogy(svi_result.losses);
Recovering Posterior Samples
As soon as the mannequin has been educated, we will can recuperate the posterior distribution of the parameters by feeding within the ensuing parameters and the preliminary dataset. We can not name the parameters svi_result.params immediately since Numpyro makes use of an affline transformation on the back-end for non-Regular distributions. Due to this fact, we pattern 1000 occasions from the posterior distribution and calculate the imply and commonplace deviation of every parameter in our mannequin. The ultimate a part of the next code creates a dataframe with the estimated elasticity for every product at every hierarchical degree, which we then be part of again to our authentic dataframe to check whether or not the algorithm recovers the true elasticity.
predictive = numpyro.infer.Predictive(
autoguide.AutoNormal(mannequin, init_loc_fn=init_to_sample),
params=svi_result.params,
num_samples=1000
)
samples = predictive(rng_key, df, df['units_sold'])
# Extract means and std dev
outcomes = {}
excluded_keys = ['product_effect', 'time_cat_effects']
for okay, v in samples.gadgets():
if okay not in excluded_keys:
outcomes[f"{k}"] = np.imply(v, axis=0)
outcomes[f"{k}_std"] = np.std(v, axis=0)
# product elasticity estimates
prod_elasticity_df = pd.DataFrame({
'product': df['product'].distinctive(),
'product_elasticity_svi': outcomes['product_a'],
'product_elasticity_svi_std': outcomes['product_a_std'],
})
result_df = df.merge(prod_elasticity_df, on='product', how='left')
# Class elasticity estimates
prod_elasticity_df = pd.DataFrame({
'class': df['category'].distinctive(),
'category_elasticity_svi': outcomes['category_a'],
'category_elasticity_svi_std': outcomes['category_a_std'],
})
result_df = result_df.merge(prod_elasticity_df, on='class', how='left')
# World elasticity estimates
result_df['global_a_svi'] = outcomes['global_a']
result_df['global_a_svi_std'] = outcomes['global_a_std']
result_df.head()
| product | class | time_period | worth | units_sold | product_elasticity | category_elasticity | global_elasticity | cat_by_time | product_elasticity_svi | product_elasticity_svi_std | category_elasticity_svi | category_elasticity_svi_std | global_a_svi | global_a_svi_std |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 8 | 0 | 125.95 | 550 | -1.185907 | -1.63475 | -1.597683 | 8-0 | -1.180956 | 0.000809 | -1.559872 | 0.027621 | -1.5550271 | 0.2952548 |
| 0 | 8 | 1 | 125.95 | 504 | -1.185907 | -1.63475 | -1.597683 | 8-1 | -1.180956 | 0.000809 | -1.559872 | 0.027621 | -1.5550271 | 0.2952548 |
| 0 | 8 | 2 | 149.59 | 388 | -1.185907 | -1.63475 | -1.597683 | 8-2 | -1.180956 | 0.000809 | -1.559872 | 0.027621 | -1.5550271 | 0.2952548 |
| 0 | 8 | 3 | 149.59 | 349 | -1.185907 | -1.63475 | -1.597683 | 8-3 | -1.180956 | 0.000809 | -1.559872 | 0.027621 | -1.5550271 | 0.2952548 |
| 0 | 8 | 4 | 176.56 | 287 | -1.185907 | -1.63475 | -1.597683 | 8-4 | -1.180956 | 0.000809 | -1.559872 | 0.027621 | -1.5550271 | 0.2952548 |
Outcomes
The next code plots the true and estimated elasticities for every product. Every level is ranked by their true elasticity worth (black), and the estimated elasticity from the mannequin can also be proven. We are able to see that the estimated elasticities follows the trail of the true elasticities, with a Imply Absolute Error of round 0.0724. Factors in crimson represents merchandise whose 95% CI doesn’t comprise the true elasticity, whereas factors in blue symbolize merchandise whose 95% CI comprises the true elasticity. On condition that the worldwide imply is -1.598, this represents a median error of 4.5% on the product degree. We are able to see that the SVI estimates carefully observe the sample of the true elasticities however with some noise, significantly because the elasticities grow to be increasingly more destructive. On the highest proper panel, we plot the connection between the error of the estimated elasticities and the true elasticity values. As true elasticities grow to be increasingly more destructive, our mannequin turns into much less correct.
For the category-level and global-level elasticities, we will create the posteriors utilizing two strategies. We are able to both boostrap all product-level elasticities inside the class, or we will get the category-level estimates immediately from the posterior parameters. After we take a look at the category-level elasticity estimates on the underside left, we will see that the each the category-level estimates recovered from the mannequin and the bootstrapped samples from the product-level elasticities are additionally barely biased in direction of zero, with an MAE of ~.033. Nonetheless, the boldness interval given by the category-level parameter covers the true parameter, not like the bootstrapped product-level estimates. This means that when figuring out group-level elasticities, we must always immediately use the group-level parameters as a substitute of bootstrapping the extra granular estimates. When wanting on the international degree, each strategies comprises the true parameter estimate within the 95% confidence bounds, with the worldwide parameter out-performing the product-level bootstrapping, at the price of having bigger commonplace errors.
Issues
- HB underestimates posterior variance: One disadvantage of utilizing SVI for the estimation is that it underestimates the posterior variance. Whereas we’ll cowl this matter intimately in a later article, the target perform for SVI solely takes into consideration the distinction in expectation of our posited distribution and the true distribution. Which means it doesn’t take into account the total correlation construction between parameters within the posterior. The mean-field approximation generally utilized in SVI assumes conditional (on the earlier hierarchy’s draw) independence between parameters, which ignores any covariances between merchandise inside the identical hierarchy. Which means if are any spillover results (corresponding to cannibalization or cross-price elasticity), it could not be accounted for within the confidence bounds. As a consequence of this mean-field assumption, the uncertainty estimates are usually overly assured, leading to confidence intervals which are too slender and fail to correctly seize the true parameter values on the anticipated fee. We are able to see within the prime left determine that solely 9.7% of the product-level elasticities cowl their true elasticity. In a later publish, we’ll embrace some options to this drawback.
- Significance of priors: When utilizing HB, priors matter considerably extra in comparison with commonplace Bayesian approaches. Whereas giant datasets usually enable the chance to dominate priors when estimating international parameters, hierarchical constructions modifications this dynamic and cut back the efficient pattern sizes at every degree. In our mannequin, the worldwide parameter solely sees 10 category-level observations (not the total dataset), classes solely draw from their contained merchandise, and merchandise rely solely on their very own observations. This diminished efficient pattern measurement causes shrinkage, the place outlier estimates (like very destructive elasticities) get pulled towards their class means. This highlights the significance of prior predictive checks, since misspecified priors can have outsized affect on the outcomes.

def elasticity_plots(result_df, outcomes=None):
# Create the determine with 2x2 grid
fig = plt.determine(figsize=(12, 10))
gs = fig.add_gridspec(2, 2)
# product elasticity
ax1 = fig.add_subplot(gs[0, 0])
# Knowledge prep
df_product = result_df[['product','product_elasticity','product_elasticity_svi','product_elasticity_svi_std']].drop_duplicates()
df_product['product_elasticity_svi_lb'] = df_product['product_elasticity_svi'] - 1.96*df_product['product_elasticity_svi_std']
df_product['product_elasticity_svi_ub'] = df_product['product_elasticity_svi'] + 1.96*df_product['product_elasticity_svi_std']
df_product = df_product.sort_values('product_elasticity')
mae_product = np.imply(np.abs(df_product.product_elasticity-df_product.product_elasticity_svi))
colours = []
for i, row in df_product.iterrows():
if (row['product_elasticity'] >= row['product_elasticity_svi_lb'] and
row['product_elasticity'] <= row['product_elasticity_svi_ub']):
colours.append('blue') # Inside CI bounds
else:
colours.append('crimson') # Exterior CI bounds
# Share of factors inside bounds
within_bounds_pct = colours.rely('blue') / len(colours) * 100
# Plot knowledge
ax1.scatter(vary(len(df_product)), df_product['product_elasticity'],
coloration='black', label='True Elasticity', s=20, zorder=3)
ax1.scatter(vary(len(df_product)), df_product['product_elasticity_svi'],
coloration=colours, label=f'SVI Estimate (MAE: {mae_product:.4f}, Protection: {within_bounds_pct:.1f}%)',
s=3, zorder=2)
ax1.set_xlabel('Product Index (sorted by true elasticity)')
ax1.set_ylabel('Elasticity Worth')
ax1.set_title('SVI Estimates of True Product Elasticities')
ax1.legend()
ax1.grid(alpha=0.3)
# Relationship between MAE and true elasticity
ax2 = fig.add_subplot(gs[0, 1])
# Calculate MAE for every product
temp = result_df[['product','product_elasticity', 'product_elasticity_svi']].drop_duplicates().copy()
temp['product_error'] = temp['product_elasticity'] - temp['product_elasticity_svi']
temp['product_mae'] = np.abs(temp['product_error'])
correlation = temp[['product_mae', 'product_elasticity']].corr()
# Plot knowledge
ax2.scatter(temp['product_elasticity'], temp['product_error'], alpha=0.5, s=5, coloration = colours)
ax2.set_xlabel('True Elasticity')
ax2.set_ylabel('Error (True - Estimated)')
ax2.set_title('Relationship Between True Elasticity and Estimation Accuracy')
ax2.grid(alpha=0.3)
ax2.textual content(0.5, 0.95, f"Correlation: {correlation.iloc[0,1]:.3f}",
remodel=ax2.transAxes, ha='middle', va='prime',
bbox=dict(boxstyle='spherical', facecolor='white', alpha=0.7))
# Class Elasticity
ax3 = fig.add_subplot(gs[1, 0])
# Distinctive classes and elasticities
category_data = result_df[['category', 'category_elasticity', 'category_elasticity_svi', 'category_elasticity_svi_std']].drop_duplicates()
category_data = category_data.sort_values('category_elasticity')
# Bootstrapped means from product elasticities inside every class
bootstrap_means = []
bootstrap_ci_lower = []
bootstrap_ci_upper = []
for cat in category_data['category']:
# Get product elasticities for this class
prod_elasticities = result_df[result_df['category'] == cat]['product_elasticity_svi'].distinctive()
# Bootstrap means
boot_means = [np.mean(np.random.choice(prod_elasticities, size=len(prod_elasticities), replace=True))
for _ in range(1000)]
bootstrap_means.append(np.imply(boot_means))
bootstrap_ci_lower.append(np.percentile(boot_means, 2.5))
bootstrap_ci_upper.append(np.percentile(boot_means, 97.5))
category_data['bootstrap_mean'] = bootstrap_means
category_data['bootstrap_ci_lower'] = bootstrap_ci_lower
category_data['bootstrap_ci_upper'] = bootstrap_ci_upper
# Calculate MAE
mae_category_svi = np.imply(np.abs(category_data['category_elasticity_svi'] - category_data['category_elasticity']))
mae_bootstrap = np.imply(np.abs(category_data['bootstrap_mean'] - category_data['category_elasticity']))
# Plot the info
left_offset = -0.2
right_offset = 0.2
x_range = vary(len(category_data))
ax3.scatter(x_range, category_data['category_elasticity'],
coloration='black', label='True Elasticity', s=50, zorder=3)
# Bootstrapped product elasticity
ax3.scatter([x + left_offset for x in x_range], category_data['bootstrap_mean'],
coloration='inexperienced', label=f'Bootstrapped Product Estimate (MAE: {mae_bootstrap:.4f})', s=30, zorder=2)
for i in x_range:
ax3.plot([i + left_offset, i + left_offset],
[category_data['bootstrap_ci_lower'].iloc[i], category_data['bootstrap_ci_upper'].iloc[i]],
coloration='inexperienced', alpha=0.3, zorder=1)
# category-level SVI estimates
ax3.scatter([x + right_offset for x in x_range], category_data['category_elasticity_svi'],
coloration='blue', label=f'Class SVI Estimate (MAE: {mae_category_svi:.4f})', s=30, zorder=2)
for i in x_range:
ci_lower = category_data['category_elasticity_svi'].iloc[i] - 1.96 * category_data['category_elasticity_svi_std'].iloc[i]
ci_upper = category_data['category_elasticity_svi'].iloc[i] + 1.96 * category_data['category_elasticity_svi_std'].iloc[i]
ax3.plot([i + right_offset, i + right_offset], [ci_lower, ci_upper], coloration='blue', alpha=0.3, zorder=1)
ax3.set_xlabel('Class Index (sorted by true elasticity)')
ax3.set_ylabel('Elasticity')
ax3.set_title('Comparability with True Class Elasticity')
ax3.legend()
ax3.grid(alpha=0.3)
# international elasticity
ax4 = fig.add_subplot(gs[1, 1])
temp = result_df[['product','product_elasticity_svi','global_elasticity']].drop_duplicates()
bootstrap_means = [np.mean(np.random.choice(np.array(temp['product_elasticity_svi']), 100)) for i in vary(10000)]
global_means = np.random.regular(result_df['global_a_svi'].iloc[0], result_df['global_a_svi_std'].iloc[0], 10000)
true_global = np.distinctive(temp.global_elasticity)[0]
p_mae = np.abs(np.imply(bootstrap_means) - true_global)
g_mae = np.abs(np.imply(global_means) - true_global)
# Plot knowledge
ax4.hist(bootstrap_means, bins=100, alpha=0.3, density=True,
label=f'Product Elasticity Bootstrap (MAE: {p_mae:.4f})')
ax4.hist(global_means, bins=100, alpha=0.3, density=True,
label=f'World Elasticity Distribution (MAE: {g_mae:.4f})')
ax4.axvline(x=true_global, coloration='black', linestyle='--', linewidth=2,
label=f'World Elasticity: {true_global:.3f}', zorder=0)
ax4.set_xlabel('Elasticity')
ax4.set_ylabel('Frequency')
ax4.set_title('World Elasticity Comparability')
ax4.legend()
ax4.grid(True, linestyle='--', alpha=0.7)
# Present
plt.tight_layout()
plt.present()
elasticity_plots(result_df)
Conclusion
Alternate Makes use of: Except for estimating worth elasticity of demand, HB fashions even have a wide range of different makes use of in Knowledge Science. In retail, HB fashions can forecast demand for current shops and clear up the cold-start drawback for brand new shops by borrowing data from shops/networks which have already been established and are clustered inside the identical hierarchy. For suggestion techniques, HB can estimate user-level preferences from a mix of consumer and item-level traits. This construction allows related suggestions to new customers primarily based on cohort behaviors, step by step transitioning to individualized suggestions as consumer historical past accumulates. If no cohort groupings are simply accessible, Okay-means can be utilized to group related models primarily based on their traits.
Lastly, these fashions will also be used to mix outcomes from experimental and observational research. Scientists can use historic observational uplift estimates (adverts uplift) and complement it with newly developed A/B assessments to cut back the required pattern measurement for experiments by incorporating prior information. This strategy creates a steady studying framework the place every new experiment builds upon earlier findings moderately than ranging from scratch. For groups going through useful resource constraints, this implies sooner time-to-insight (particularly when mixed with surrogate fashions) and extra environment friendly experimentation pipelines.
Closing Remarks: Whereas this introduction has highlighted a number of functions of hierarchical Bayesian fashions, we’ve solely scratched the floor. We haven’t deep dived into granular implementation features corresponding to prior and posterior predictive checks, formal goodness-of-fit assessments, computational scaling, distributed coaching, efficiency of estimation methods (MCMC vs. SVI), and non-nested hierarchical constructions, every of which deserves their very own publish.
Nonetheless, this overview ought to present a sensible place to begin for incorporating hierarchical Bayesian into your toolkit. These fashions supply a framework for dealing with (normally) messy, multi-level knowledge constructions which are usually seen in real-world enterprise issues. As you start implementing these approaches, I’d love to listen to about your experiences, challenges, successes, and new use circumstances for this class of mannequin, so please attain out with questions, insights, or examples via my electronic mail or LinkedIn. When you’ve got any suggestions on this text, or wish to request one other matter in causal inference/machine studying, please additionally be happy to succeed in out. Thanks for studying!
Note: All photos used on this article is generated by the writer.